Samacheer Kalvi 10th Maths Guide Chapter 3 Algebra Ex 3.2

Students can download Maths Chapter 3 Algebra Ex 3.2 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.2

Question 1.
Find the GCD of the given polynomials by Division Algorithm
(i) x⁴ + 3x³ – x – 3, x³ + x² – 5x + 3
Answer:
p(x) = x⁴ + 3x³ – x – 3
g(x) = x³ + x² – 5x + 3

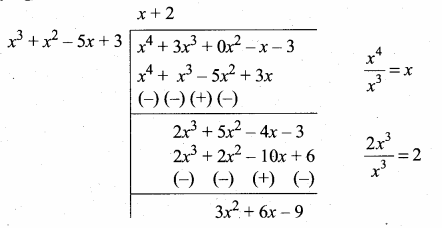
3x² + 6x – 9 = 3(x² + 2x – 3)
Now dividing g(x) = x³ + x² – 5x + 3
by the new remainder
(leaving the constant 3)
we get x² + 2x – 3
G.C.F. = x² + 2x – 3

(ii) x⁴ – 1, x³ – 11x² + x – 11
p(x) = x⁴ – 1
g(x) = x³ – 11x² + x – 11

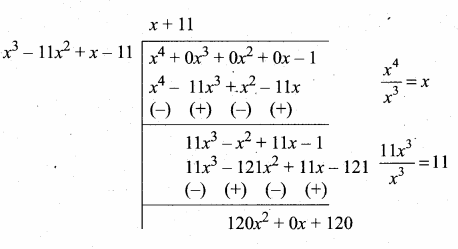
120x² + 120 = 120 (x² + 1)
Now dividing g(x) = x³ – 11x² + x – 11 by the new remainder (leaving the constant) we get x² + 1

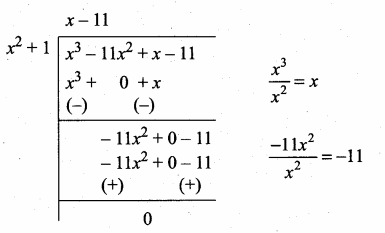
G.C.D. = x² + 1

(iii) 3x⁴ + 6x³ – 12x² – 24x, 4x⁴ + 14x³ + 8x² – 8x
Answer:
p(x) = 3x⁴ + 6x³ – 12x² – 24x
= 3x (x³ + 2x² – 4x – 8)
g(x) = 4x⁴ + 14x³ + 8x² – 8x
= 2x (2x³ + 7x² + 4x – 4)
G.C.D. of 3x and 2x = x
Now g(x) is divide by p(x) we get

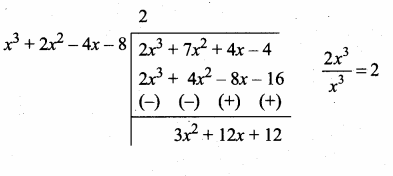
3x² + 12x + 12 = 3 (x² + 4x + 4)
Now dividing p(x) = x³ + 2x² – 4x – 8
by the new remainder
(leaving the constant)
x² + 4x + 4

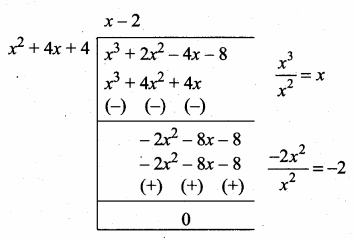
G.C.D. = x(x² + 4x + 4) [Note x is common for p(x) and g(x)]

(iv) 3x³ + 3x² + 3x + 3, 6x³ + 12x² + 6x+12
p(x) = 3x³ + 3x² + 3x + 3
= 3(x³ + x² + x + 1)
g(x) = 6x³ + 12x² + 6x + 12
= 6(x³ + 2x² + x + 2)
G.C.D. of 3 and 6 = 3
Now g(x) is divided by p(x)

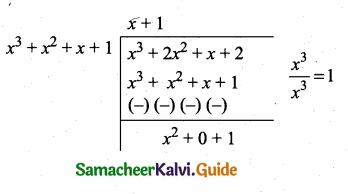
Now dividing p(x) by the remainder x² + 1
we get x + 1

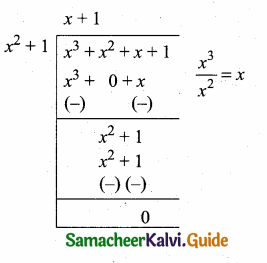
∴ G.C.D. = 3(x² + 1) [3 is the G.C.D. of 3 and 6]

Question 2.
Find the LCM of the given polynomials
(i) 4x²y, 8x³y²
Answer:
4x² y = 2 × 2 × x² × y
8 x³ y² = 2 × 2 × 2 × x³ × y²
L.C.M. = 2³ × x³ × y²
= 8x³y²

Aliter: L.C.M of 4 and 8 = 8
L.C.M. of x²y and x³y² = x³y²
∴ L.C.M. = 8x³y²

(ii) -9a³b², 12a²b²c
Answer:
-9a³b² = -(3² × a³ × b²)
12a²b²c = 2² × 3 × a² × b² × c
L.C.M. = -(2² × 3² × a³ × b² × c)
= -36 a³b²c

(iii) 16m, -12m²n², 8n²
Answer:
16m = 24 × m
-12 m²n² = -(2² × 3 × m² × n²)
8n² = 2³ × n²
L.C.M. = -(2⁴ × 3 × m² × n²)
= -48 m²n²

(iv) p² – 3p + 2, p² – 4
Answer:
P² – 3p + 2 = p² – 2p – p + 2
= p(p – 2) – 1 (p – 2)
= (p – 2) (p – 1)

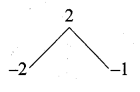
p² – 4 = p² – 2² (using a² – b² = (a + b) (a – b)]
= (p + 2) (p – 2)
L.C.M. = (p – 2) (p + 2) (p – 1)

(v) 2x² – 5x – 3,4.x² – 36
Answer:
2x² – 5x – 3 = 2x² – 6x + x – 3
= 2x (x – 3) + 1 (x – 3)
= (x – 3) (2x + 1)

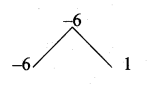
= 4x² – 36 = 4 [x² – 9]
= 4 [x² – 3²]
= 4(x + 3) (x – 3)
L.C.M. = 4(x – 3) (x + 3) (2x + 1)

(vi) (2x² – 3xy)²,(4x – 6y)³,(8x³ – 27y³)
Answer:
(2x² – 3xy)² = x² (2x – 3y)²
(4x – 6y)³ = 2³ (2x – 3y)³
= 8 (2x – 3y)³
8x³ – 27y³ = (2x)³ – (3y)³
= (2x – 3y) [(2x)² + 2x × 3y + (3y²)]
[using a³ – b³ = (a – b) (a² + ab + b²)
(2x – 3y) (4x² + 6xy + 9y²)
L.C.M. = 8x² (2x – 3y)³ (4x² + 6xy + 9y)²