Students can download Maths Chapter 3 Algebra Ex 3.15 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.15
Question 1.
Graph the following quadratic equations and state their nature of solutions.
(i) x2 – 9x + 20 = 0
(ii) x2 – 4x + 4 = 0
(iii) x2 + x + 7 = 0
(iv) x2 – 9 = 0
(v) x2 – 6x + 9 = 0
(vi) (2x – 3) (x + 2) = 0
(i) x2 – 9x + 20 = 0
Answer:
Let y = x2 – 9x + 20
(i) Prepare the table of values for y = x2 – 9x + 20
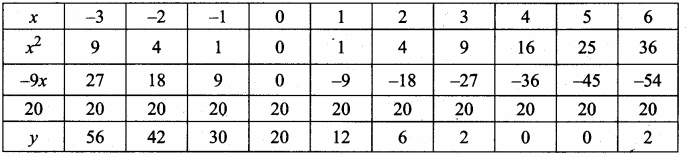
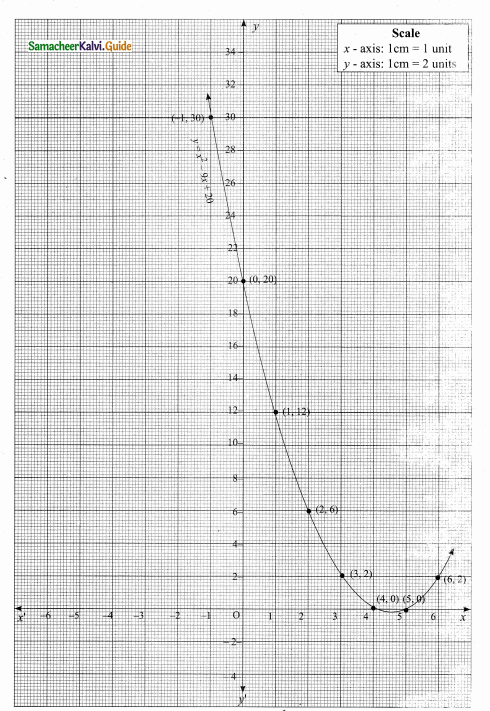
(ii) Plot the points (-1, 30) (0,20) (1, 12) (2, 6) (3,2), (4, 0), (5, 0), (6,2) (omit the high value)
(iii) Join the points by a free hand smooth curve.
(iv) The roots of the equation are the X-coordinates of the intersecting points of the curve with X-axis (4, 0) and (5, 0)
There are two points of intersection with the X-axis at 4 and 5. The solution set is 4 and 5. The quadratic equation has real and unequal roots.
(v) Since there is two point of intersection with X-axis (different solution)
∴ The equation x2 – 9x + 20 = 0 has real and unequal roots.
![]()
(ii) x2 – 4x + 4 = 0
Answer:
Let y = x2 – 4x + 4
(i) Prepare the table of values for y = x2 – 4x + 4
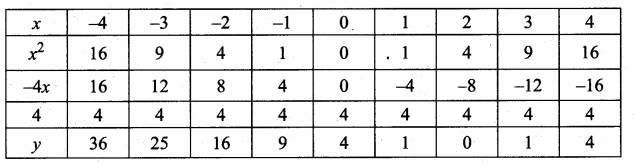
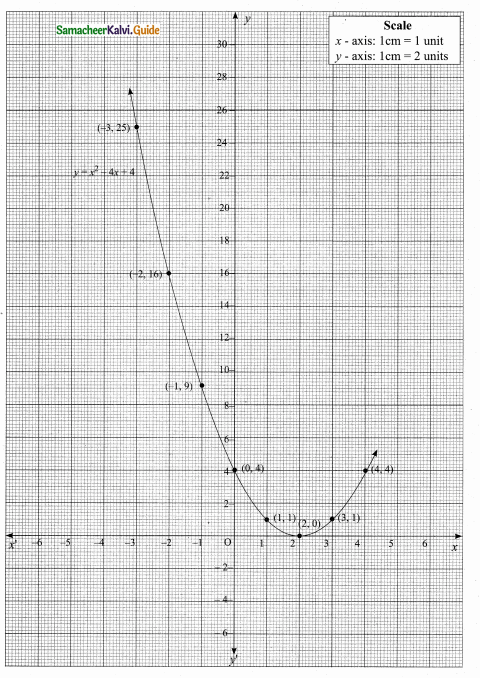
(ii) Plot the points (-3,25) (-2,16) (-1, 9) (0,4) (1,-1) (2, 0), (3,1) and (4, 4)
(iii) Join the points by a free hand smooth curve.
(iv) The roots of the equation are the X-coordinates of the intersecting points of the curve with X-axis (2, 0) which is 2.
(v) Since there is only one point of intersection with X-axis (2, 0).
∴ The solution set is 2.
The Quadratic equation x2 – Ax + 4 = 0 has real and equal roots.
(iii) x2 + x + 7 = 0
Answer:
Let y = x2 + x + 7
(i) Prepare the table of values for y = x2 + x + 7
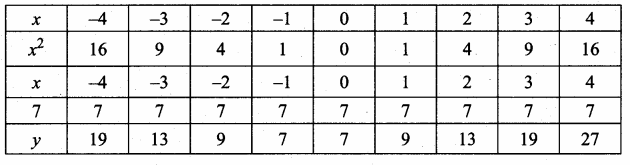
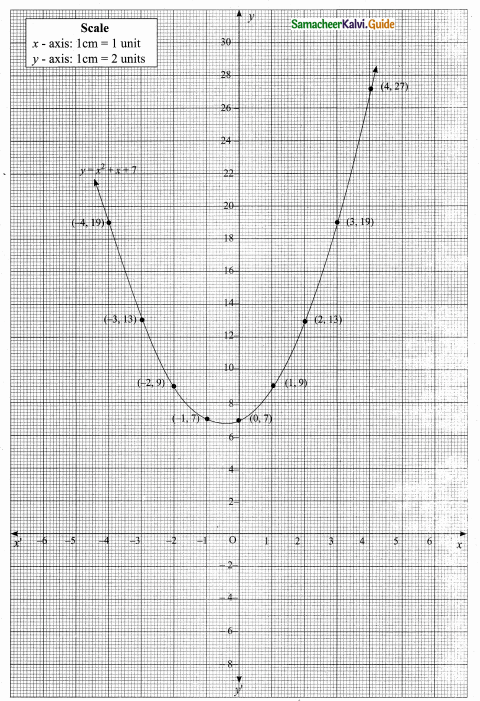
(ii) Plot the points (-4,19) (-3,13) (-2, 9) (-1, 7) (0, 7) (1, 9), (2,13) (3,19) and (4,27)
(iii) Join the points by a free hand smooth curve.
(iv) The solution of the given quadratic equation are the X-coordinates of the intersecting points of the parabola with the X-axis.
(v) The curve does not intersecting the X-axis. There is no solution set.
The equation x2 + x + 7 = 0 has no real roots.
![]()
(iv) x2 – 9 = 0
Answer:
Let y = x2 – 9
(i) Prepare the table of values for y = x2 – 9
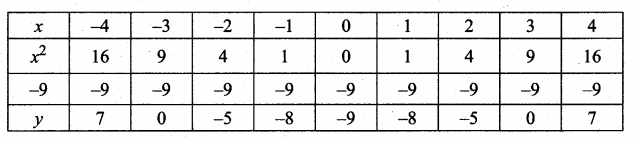
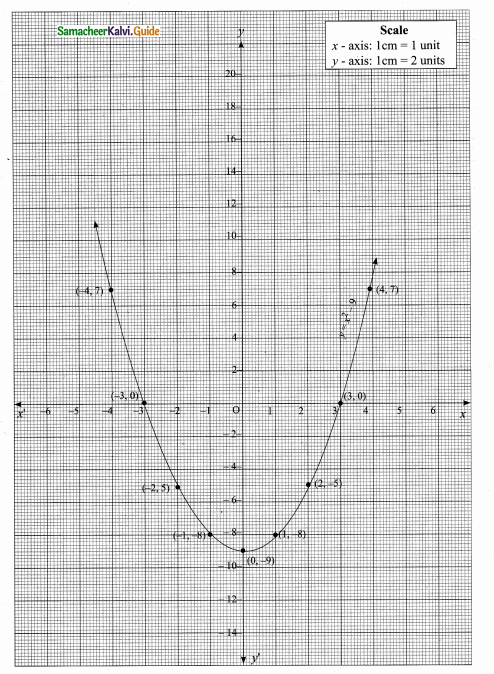
(ii) Plot the points (-4, 7) (-3, 0) (-2, -5) (-1, -8) (0, -9) (1, -8), (2, -5) (3, 0) (4, 7)
(iii) Join the points by a free hand smooth curve.
(iv) The curve intersect the X-axis at -3 and 3.
The solution is (-3, 3).
(v) Since there are two points of intersection -3 and 3 with the X-axis the quadratic equation has real and unequal roots.
![]()
(v) x2 – 6x + 9 = 0
Answer:
Let y = x2 – 6x + 9
(i) Prepare a table of values for y = x2 – 6x + 9
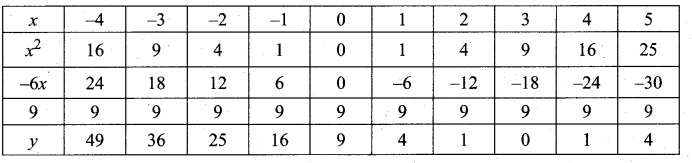
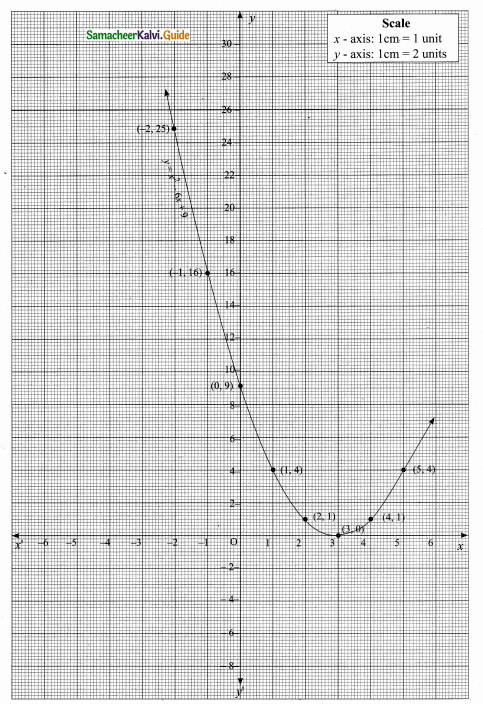
(ii) Plot the points (-2,25) (-1,16) (0,9) (1,4) (2,1) (3,0), (4,1) and (5,4) on the graph using suitable scale (omit the points (-4, 49) and (-3, 36)
(iii) Join the points by a free hand smooth curve.
(iv) The X – coordinates of the point of intersection of the curve with X-axis are the roots of the , given equation, provided they intersect.
The solution is 3.
(v) Since there is only one point of intersection with X-axis the quadratic equation x2 – 6x + 9 = 0 has real and equal roots.
![]()
(vi) (2x – 3) (x + 2) = 0
Answer:
y = (2x – 3) (x + 2)
= 2x2 + 4x – 3x – 6
= 2x2 + x – 6
(i) Prepare a table of values for y from x – 4 to 4
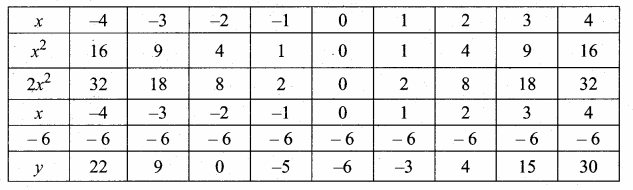
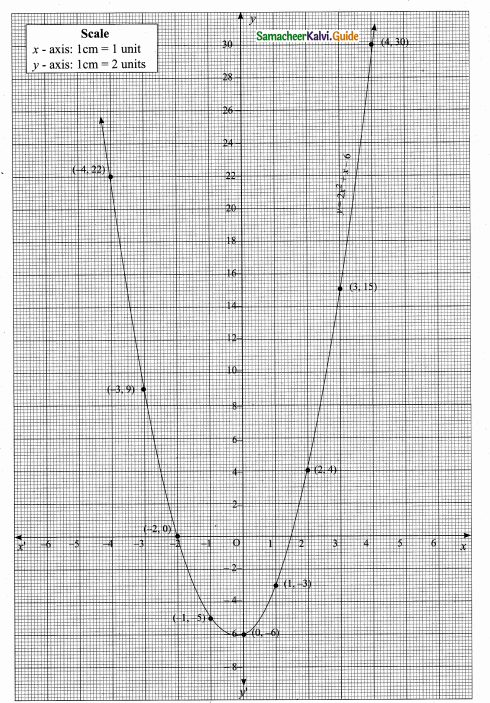
(ii) Plot the points (-4, 22) (-3, 9) (-2, 0) (-1, -5) (0, -6) (1, -3), (2, 4), (3, 15) and (4, 30).
(iii) Join the points by a free hand smooth curve.
(iv) The curve intersect the X – axis at (-2, 0) and (1\(\frac { 1 }{ 2 } \), 0)
∴ The solution set is (-2,1\(\frac { 1 }{ 2 } \))
(v) Since there are two points of intersection with X – axis, the quadratic equation has real and un – equal roots.
![]()
Question 2.
Draw the graph of y = x2 – 4 and hence solve x2 – x – 12 = 0
Answer:
(i) Draw the graph of y = x2 – 4 by preparing the table of values as below.
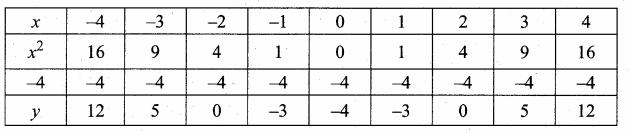
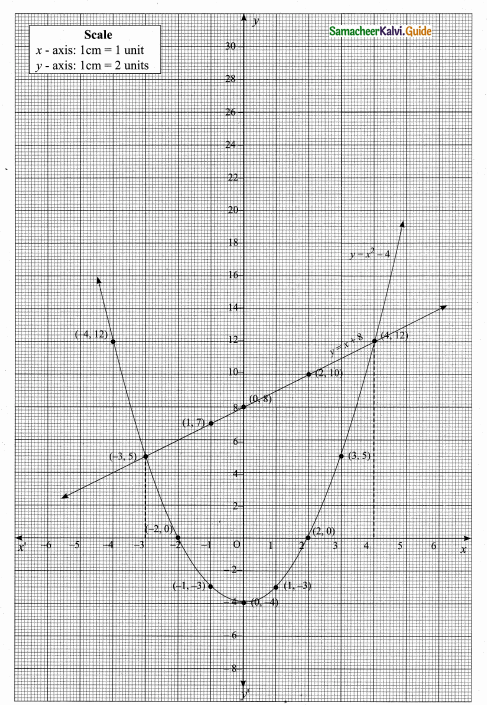
(ii) Plot the points for the ordered pairs (-4, 12) (-3, 5) (-2, 0) (-1, -3) (0, -4) (1, -3), (2, 0), (3, 5) and (4, 12). Draw the curve with the suitable scale.
(iii) To solve x2 – x – 12 = 0 subtract x2 – x – 12 from y = x2 – 4
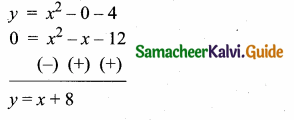
The equation y = x + 8 represents a straight line. Prepare a table for y = x + 8

(iv) Mark the point of intersection of the curve and the straight line is (-3, 5) and 4, 12)
∴ The solution set is (-3, 4) for x2 – x – 12 = 0.
![]()
Question 3.
Draw the graph of y = x2 + x and hence solve x2 + 1 = 0
Answer:
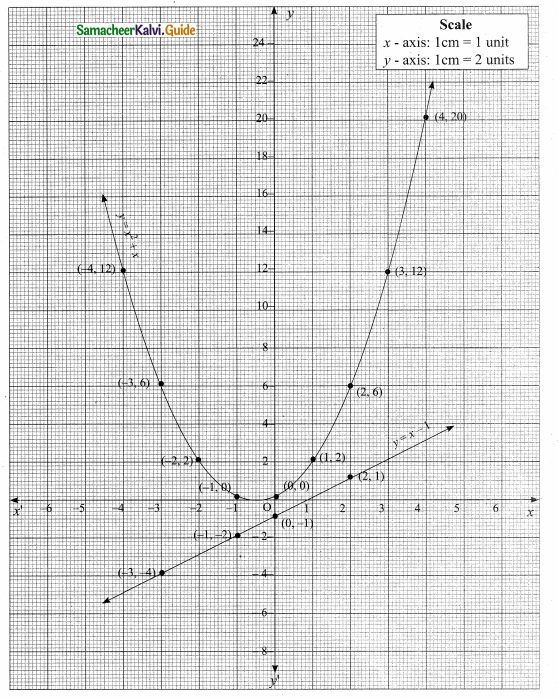
Let y = x2 + x
(i) Draw the graph of y = x2 + x by preparing the table.

(ii) Plot the points (-4, 12), (-3, 6), (-2, 2), (-1, 0), (0, 0), (1, 2), (2, 6), (3, 12) and (4, 20).
(iii) Join the points by a free hand to get smooth curve.
(iv) To solve x2 + 1 = 0, subtract x2 + 1 = 0 from x2 + x we get.
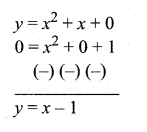
The equation represent a straight line. Draw a line y = x – 1
Observe the graph of y = x2 + 1 does not interset the parabola y = x2 + x.
This x2 + 1 has no real roots.
![]()
Question 4.
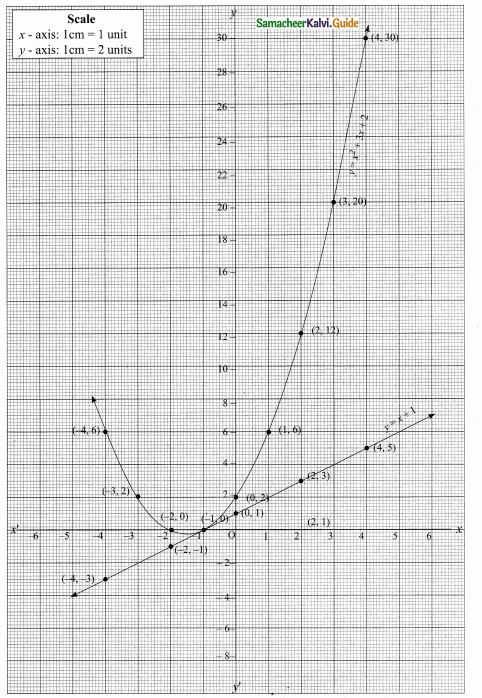
Draw the graph of y = x2 + 3x + 2 and use it to solve x2 + 2x + 1 = 0.
(i) Draw the graph of y = x2 + 3x + 2 preparing the table of values as below.
(ii) Plot the points (-4, 6), (-3, 2), (-2, 0), (-1, 0), (0, 2), (1, 6), (2, 12), (3, 20) (4, 30).
(iii) To solve x2 + 2x + 1 = 0 subtract x2 + 2x + 1 = 0 from y = x2 + 3x + 2

(iv) Draw the graph of y = x + 1 from the table

The equation y = x + 1 represent a straight line.
This line intersect the curve at only one point (-1, 0). The solution set is (-1).
![]()
Question 5.
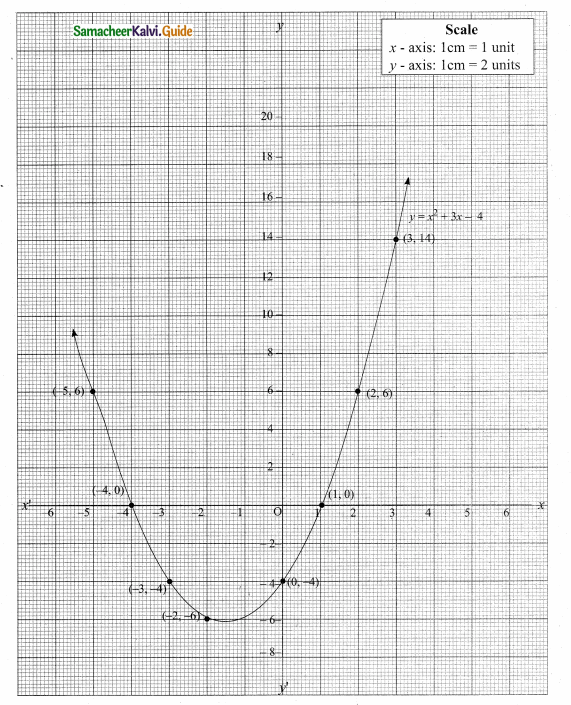
Draw the graph of y = x2 + 3x – 4 and hence use it to solve x2 + 3x – 4 = 0
Answer:
Let y = x2 + 3x – 4
(i) Draw the graph of y = x2 + 3x – 4
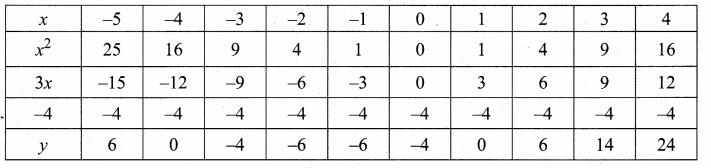
(ii) Plot the points (-5, 6), (-4, 0), (-3, -4), (-2, -6), (-1, -6), (0, -4), (1, 0), (2, 6), (3, 14) on the graph using suitable scale.
(iii) Join the points by a free hand smooth curve.
The smooth curve is the graph of y = x2 – 4x + 4
(iv) To solve x + 3x – 4 = 0, subtract x2 + 3x – 4 = 0 from y = x2 + 3x – 4.
y = 0
∴ The point of intersection with the x – axis is the solution set.
The solution set is -4 and 1.
Question 6.
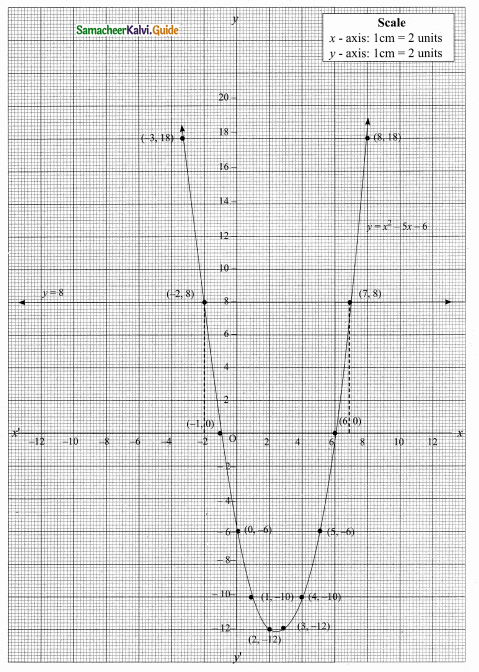
Draw the graph of y = x2 – 5x – 6 and hence solve x2, – 5x – 14 = 0
Answer:
Let y = x2 – 5x – 6
(i) Draw the graph of y = x2 – 5x – 6 by preparing the table of values as below.
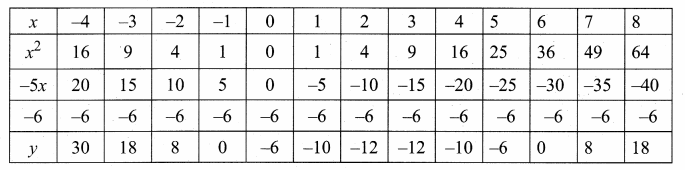
(ii) Plot the points (-3, 18), (-2, 8), (-1, 0), (0, -6), (1, -10), (2, -12), (3, -12), (4, -10), (5,-6), (6, 0) and (7, 8).
(iii) Join the points by a free hand to get smooth curve.
(iv) To solve x2 – 5x – 14 = 0, subtract x2 – 5x – 14 = 0 from y = x2 – 5x – 6.
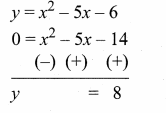
The equation y = 8 represent a straight line draw a straight line through y = 8 intersect the curve at two places. From the two points draw perpendicular line to the X – axis it will intersect at -2 and 7.
The solution is -2 and 7
![]()
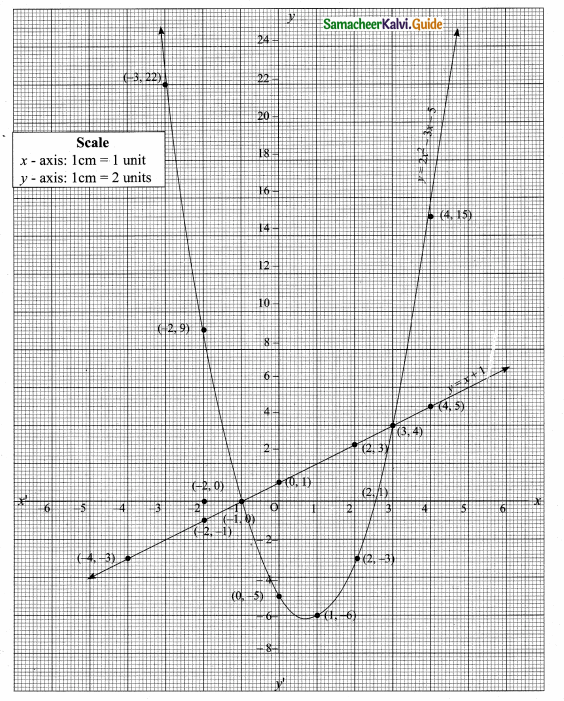
Question 7.
Draw the graph of y = 2x2 – 3x – 5 and hence solve 2x2 – 4x – 6 = 0
Answer:
(i) Draw the graph of y = 2x2 – 3x – 5 by preparing the table of values given below.
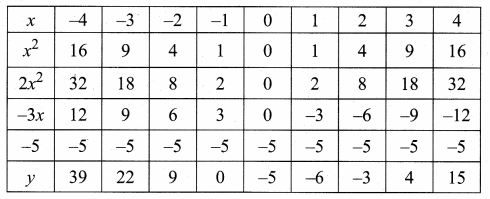
(ii) Plot the points (-3, 22), (-2, 9), (-1, 0), (0, -5), (1,-6), (2, -3), (3, 4), (4, 15) on the graph sheet using suitable scale.
(iii) To solve 2x2 – 4x – 6 = 0 subtract 2x2 – 4x – 6 = 0 from y = 2x2 – 3x – 5
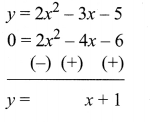
(iv) y = x + 1 represent a straight line.
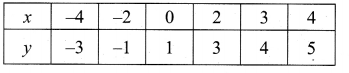
The straight line intersect the curve at (-1, 0) and (3, 4). From the two point draw perpendicular lines to the X – axis it will intersect at -1 and 3.
The solution set is (-1, 3)
![]()
Question 8.
Draw the graph of y = (x – 1) (x + 3) and hence solve x2 – x – 6 = 0
Answer:
y = (x – 1) (x + 3)
y = x2 + 2x – 3
(i) Draw the graph of y = x2 + 2x – 3 by preparing the table of values given below
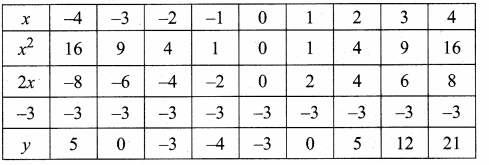
(ii) Plot the points (-4, 5), (-3, 0), (-2, -3), (-1, -4), (0, -3), (1, 0), (2, 5), (3, 12) and (4, 21) on the graph sheet using suitable scale.
(iii) To solve x2 – x – 6 = 0 subtract x2 – x – 6 = 0 from y = x2 + 2x – 3
(iv) Draw the graph of y = 3x + 3 by preparing the table.
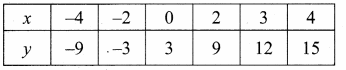
(v) The straight line cuts the curve at (-2, -3) and (3, 12). Draw perpendicular lines from the point to X – axis.
The line cut the X – axis at -2 and 3.
The solution set is (-2, 3)