Samacheer Kalvi 10th Maths Guide Chapter 2 Numbers and Sequences Ex 2.2

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.2 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.2

Question 1.
For what values of natural number n, 4th can end with the digit 6?
Answer:
4n = (2²)ⁿ = 2²ⁿ
= 2ⁿ × 2ⁿ
2 is a factor of 4ⁿ
∴ 4ⁿ is always even.

Question 2.
If m, n are natural numbers, for what values of m, does 2ⁿ × 5ⁿ ends in 5?
Solution:
2ⁿ × 5^m
2ⁿ is always even for all values of n.
5^m is always odd and ends with 5 for all values of m.
But 2ⁿ × 5^m is always even and ends in 0.
∴ 2ⁿ × 5^m cannot end with the digit 5 for any values of m. No value of m will satisfy 2ⁿ × 5^m ends in 5.

Question 3.
Find the H.C.F. of 252525 and 363636.
Answer:
To find the HCF of 252525 and 363636 by using Euclid’s Division algorithm.
363636 = 252525 × 1 + 111111
The remainder 111111 ≠ 0
By division of Euclid’s algorithm
252525 = 111111 × 2 + 30303
The remainder 30303 ≠ 0
Again by division of Euclid’s algorithm
111111 = 30303 × 3 + 20202
The remainder 20202 ≠ 0
Again by division of Euclid’s algorithm.
30303 = 20202 + 10101
The remainder 10101 ≠ 0
Again by division of Euclid’s algorithm.
20202 = 10101 × 2 + 0
The remainder is 0
∴ The H.C.F. is 10101

Question 4.
If 13824 = 2^a × 3^b then find a and b?
Answer:
Using factor tree method factorise 13824


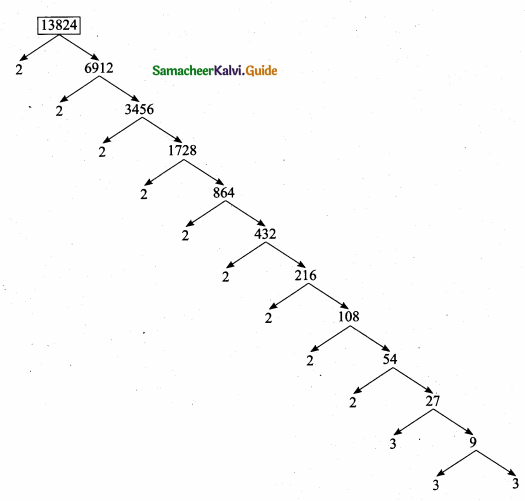
13824 = 2⁹ × 3³
Given 13824 = 2a × 3b
Compare we get a = 9 and b = 3

Aliter:
13824 = 2⁹ × 3³
Compare with
13824 = 2^a × 3^b
The value of a = 9 b = 3

Question 5.
If p₁^x1 × p₂^x2 × p₃^x3 × p₄^x4 = 113400 where p₁ p₂, p₃, p₄ are primes in ascending order and x₁, x₂, x₃, x₄, are integers, find the value of p₁,p₂,p₃,p₄ and x₁,x₂,x₃,x₄.
Answer:
Given 113400 = p₁^x1 × p₂^x2 × p₃^x3 × p₄^x4
Using tree method factorize 113400

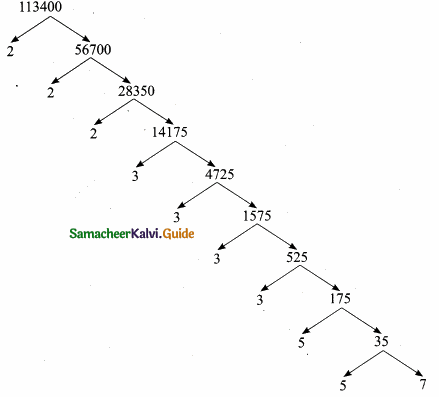
113400 = 23 × 34 × 52 × 7
compare with
113400 = p₁^x1 × p₂^x2 × p₃^x3 × p₄^x4
P₁ = 2, x₁ = 3
P₂ = 3, x₂ = 4
P₃ = 5, x₃ = 2
P₄ = 7, x₄ = 1

Question 6.
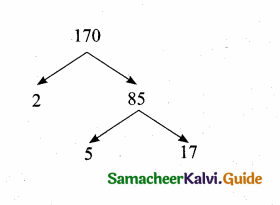
Find the L.C.M. and H.C.F. of 408 and 170 by applying the fundamental theorem of Arithmetic.
Answer:
Factorise 408 and 170 by factor tree method


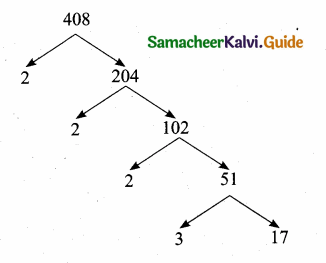
408 = 2³ × 3 × 17
170 = 2 × 5 × 17
To find L.C.M. list all prime factors of 408 and 170 of their greatest exponents.
L.C.M. = 2³ × 3 × 5 × 17
= 2040
To find the H.C.F. list all common factors of 408 and 170.
H.C.F. = 2 × 17 = 34
L.C.M. = 2040 ; HCF = 34

Question 7.
Find the greatest number consisting of 6 digits which is exactly divisible by 24,15,36?
Answer:
The greatest number of 6 digits is 999999.
The greatest number must be divisible by L.C.M. of 24, 15 and 36

24 = 2³ × 3
15 = 3 × 5
36 = 2² × 3²
L.C.M = 2³ × 3² × 5
= 360
To find the greatest number 999999 must be subtracted by the remainder when 999999 is divided by 360
The greatest number in 6 digits = 999999 – 279
= 999720

Question 8.
What is the smallest number that when divided by three numbers such as 35, 56 and 91 leaves remainder 7 in each case?
Solution:
35 = 5 × 7
56 = 2 × 2 × 2 × 7
91 = 7 × 13
LCM of 35, 56, 91 = 5 × 7 × 2 × 2 × 2 × 13 = 3640
∴ Required number = 3647 which leaves remainder 7 in each case.

Question 9.
Find the least number that is divisible by the first ten natural numbers?
Answer:
Find the L.C.M of first 10 natural numbers

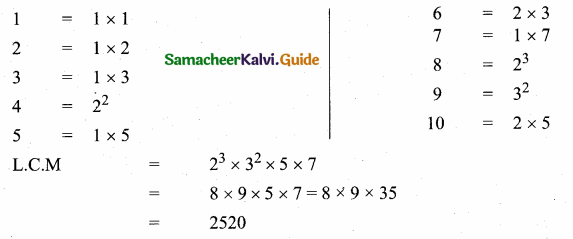
The least number is 2520

Modular Arithmetic
Two integers “a” and “b” are congruence modulo n if they differ by an integer multiple of n. That b – a = kn for some integer k. This can be written as a = b (mod n).

Euclid’s Division Lemma and Modular Arithmetic

Let m and n be integers, where m is positive. By Euclid’s division Lemma we can write n = mq + r where 0 < r < m and q is an integer.
This n = r (mod m)