Samacheer Kalvi 10th Maths Guide Chapter 2 Numbers and Sequences Additional Questions

Students can download Maths Chapter 2 Numbers and Sequences Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Additional Questions

I. Choose the correct answer.

Question 1.
The sum of the exponents of the prime factors in the prime factorisation of 504 is ……….
(1) 3
(2) 2
(3) 1
(4) 6
Answer:
(4) 6

Hint: 504 = 2³ × 3² × 7¹
Sum of the exponents
= 3 + 2 + 1 = 6

Question 2.
If two positive integers a and 6 are expressible in the form a = pq² and b = p³q ; p, q being prime numbers, then L.C.M. of (a, b) is ……………
(i) pq
(2) P² q²
(3) p³ q³
(4) P³ q²
Answer:
(4) P³ q²
Hint: a = p × q² and b = p³ × q
∴ L.C.M. of (a, b) is p³ q²

Question 3.
If n is a natural number then 7³ⁿ – 4³ⁿ is always divisible by …………….
(1) 11
(2) 3
(3) 33
(4) both 11 and 3
Answer:
(4) both 11 and 3
Hint: 7³ⁿ – 4³ⁿ is of the form a²ⁿ – b²ⁿ which is divisible by both a – b and a + b. So 7³ⁿ – 4³ⁿ is divisible by both 7 – 4 = 3 and 7 + 4 = 11.

Question 4.
The value of x when 200 = x (mod 7) is …………………
(1) 3
(2) 4
(3) 54
(4) 12
Answer:
(2) 4
Hint:

200 ≡ x (mod 7)
200 ≡ 4 (mod 7)
The value of x = 4

Question 5.
The common difference of the A.P.
\(\frac { -2 }{ 2b } \) , \(\frac { 1-6b }{ 2b } \), \(\frac { 1-12b }{ 2b } \) is …………….
(1) 2b
(2) -2b
(3) 3
(4) -3
Answer:
(4) -3
Hint:
\(\frac { 1-12b }{ 2b } \) – \(\frac { 1-6b }{ 2b } \) = \(\frac { 1-12b-1+6b }{ 2b } \) = \(\frac { -6b2 }{ 2b } \) = \(\frac { -6b }{ 2b } \) = -3

Question 6.
Which one of the following is not true?
(1) A sequence is a real valued function defined on N.
(2) Every function represents a sequence.
(3) A sequence may have infinitely many terms.
(4) A sequence may have a finite number of terms.
Answer:
(2) Every function represents a sequence.
Hint: A sequence is a function whose domain is the set of natural numbers.

Question 7.
The 8^th term of the sequence 1,1,2,3,5,8, ………. is ……….
(1) 25
(2) 24
(3) 23
(4) 21
Answer:
(4) 21
Hint: In fibonacci sequence
F_n = F_n-1 + F_n-2
F₈ = F₇ + F₆
8^th term = 6^th term + 7^th term
= 8 + (5 + 8) = 21

Question 8.
The next term of \(\frac { 1 }{ 20 } \) in the sequence \(\frac { 1 }{ 2 } \),\(\frac { 1 }{ 6 } \),\(\frac { 1 }{ 12 } \),\(\frac { 1 }{ 20 } \) is ……………
(1) \(\frac { 1 }{ 24 } \)
(2) \(\frac { 1 }{ 22 } \)
(3) \(\frac { 1 }{ 30 } \)
(4) \(\frac { 1 }{ 18 } \)
Answer:
(3) \(\frac { 1 }{ 30 } \)
Hint:
The general term t_n = \(\frac{1}{n(n+1)}\)
⇒ t₅ = \(\frac{1}{5(6)}\) = \(\frac { 1 }{ 30 } \)

Question 9.
If a, 6, c, l, m are in A.P, then the value of a – 46 + 6c – 4l + m is …………
(1) 1
(2) 2
(3) 3
(4) 0
Answer:
(4) 0
Hint: Given, a, b, c, l, m, are in A.P.
a = a; b = a + d; c = a + 2 d; 1 = a + 3d;
m = a + 4d [The general form of A.P.]
a – 4b + 6c – 4l + m
= a – 4(a + d) + 6(a + 2d) – 4 (a + 3d) + a + 4d
= a – 4a – 4d+ 6a + 12 d – 4a – 12d + a + 4d
= a + 6a + a – 4a – 4a
= 8a – 8a
= 0

Question 10.
If a, b, c are in A.P. then \(\frac { a-b }{ b-c } \) is equal to ……………
(1) \(\frac { a }{ b } \)
(2) \(\frac { b }{ c } \)
(3) \(\frac { a }{ c } \)
(4) 1
Answer:
(4) 1
Hint: a, b, c are in A.P.
b – a = c-b [common difference is same t₂ – t₁ = t₃ – t₂]
\(\frac { b-a }{ c-b } \) = 1 ⇒ \(\frac{-(a-b)}{-(b-c)}\) = 1
∴ \(\frac { a-b }{ b-c } \) = 1

Question 11.
If the n^th term of a sequence is 100n + 10, then the sequence is ……
(1) an A.P.
(2) a G..P.
(3) a constant sequence
(4) neither A.P. nor G.P.
Answer:
(1) an A.P.
Hint: t_n = 100/n + 10
t₁ = 100 + 10 = 110
t₂ = 200+ 10 = 210
t₃ = 300+ 10 = 310
∴ The series 110, 210, 310 …………. are in A.P.

Question 12.
If a₁, a₂, a₃, …… are in A.P. such that \(\frac{a_{4}}{a_{7}}=\frac{3}{2}\), then the 13th term of the A.P. is ……………..
(1) \(\frac { 3 }{ 2 } \)
(2) 0
(3) 12a1
(4) 14a1
Answer:
(2) 0
Hint:
\(\frac{a_{4}}{a_{7}}=\frac{3}{2}\)
2a₄ = 3a₇
2(a + 3d) = 3(a + 6d)
2a + 6d = 3a + 18d
0 = a + 12d
[t_n = a + (n – 1)d]
0 = t₁₃

Question 13.
If the sequence a₁, a₂, a₃ ,… is in A.P., then the sequence a₅, a₁₀, a₁₅, …. is …..,
(1) a G.P.
(2) an A.P.
(3) neither A.P nor G.P.
(4) a constant sequence
Answer:
(2) an A.P.
Hint: a₅, a₁₀, a₁₅, ……….. = a + 4d, a + 9d, a + 14d
t₂ – t₁ = a + 9d – (a + 4d) = 5d
t₃ – t₂ = a + 14d – (a + 9d) = 5d
Common difference is 5d
If terms of an A.P are chosen at equal intervals then they form an A.P.

Question 14.
If k + 2,4k – 6, 3k – 2 are the 3 consecutive terms of an A.P, then the value of K is ……………
(1) 2
(2) 3
(3) 4
(4) 5
Answer:
(2) 3
Hint: Here, a = k + 2, b = 4k-6, c = 3k-2
We know that a, b, c are in A.P.
b – a = c – b ⇒ 2b = a + c
2(4k – 6) = k + 2 + 3k – 2
8k – 12 = 4k ⇒ 4k = 12
K = \(\frac { 12 }{ 4 } \) = 3

Question 15.
If a, b, c, l, m, n are in A.P, then 3a + 7, 3b + 7, 3c + 7, 31 + 7, 3m + 7, 3n + 7 form ………..
(1) a G . P.
(2) an A.P.
(3) a constant sequence
(4) neither A.P. nor G.P.
Answer:
(2) an A.P.
Hint: In an A.P, if each term is multiplied by a constant or added by a constant, the resulting sequence is an A.P.

Question 16.
If the third term of a G.P. is 2, then the product of first 5 terms is ……………..
(1) 5²
(2) 2⁵
(3) 10
(4) 15
Answer:
(2) 2⁵
Hint: Consider the 5 terms of the G.P be \(\frac{a}{r^{2}}\),\(\frac { a }{ r } \), a, ar, ar²
Product of 5 terms = \(\frac{a}{r^{2}} \times \frac{a}{r} \times a \times a r \times ar^{2}\), = a⁵, 2⁵ (Given a = 2)

Question 17.
If a, b, c are in G.P., then \(\frac { a-b }{ b-c } \) is equal to …………..
(1) \(\frac { a }{ b } \)
(2) \(\frac { b }{ a } \)
(3) \(\frac { a }{ c } \)
(4) \(\frac { c }{ b } \)
Ans.
(1) \(\frac { a }{ b } \)
Hint: Let the common ratio be “r”

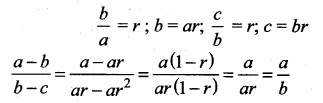
Question 18.
If x, 2x + 2, 3x + 3, are in G.P., then 5x, 10x + 10, 15x + 15, form …………..
(1) anA.P.
(2) a G.P.
(3) a constant sequence
(4) neither A.P. nor a G.P.
Answer:
(2) a G.P.
Hint: If a G.P. is multiplied by a constant then the sequence is also a G.P.
In the given question each term is multiplied by 5

Question 19.
The sequence – 3, – 3, – 3, …… is ……..
(1) an A.P. only
(2) a G.P. only
(3) neither A.P. nor G.P.
(4) both A.P. and G.P.
Answer:
(4) both A.P. and G.P.
Hint: The given sequence is constant.
The sequence is A.P. and G.P.

Question 20.
If the product of the first four consecutive terms of a G.P is 256 and if the common ratio is 4 and the first term is positive, then its 3^rd term is …….
(1) 8
(2) \(\frac { 1 }{ 16 } \)
(3) \(\frac { 1 }{ 32 } \)
(4) 16
Answer:
(1) 8
Hint: The general form of the G.P. is a, ar, ar², ar³, ar⁴, …………..
By data, a (ar) (ar²) (ar³) = 256
a⁴ × r⁶ = 256
[Given r = 4]

Question 21.
In G.P, t₂ = \(\frac { 3 }{ 5 } \) and t₃ = \(\frac { 1 }{ 5 } \) Then the common ratio is ……….
(1) \(\frac { 1 }{ 5 } \)
(2) \(\frac { 1 }{ 3 } \)
(3) 1
(4) 5
Answer:
(2) \(\frac { 1 }{ 3 } \)
Hint: common ratio is
(r) = \(\frac{t_{3}}{t_{2}}=\frac{1}{5} \times \frac{5}{3} \Rightarrow r=\frac{1}{3}\)

Question 22.
If x ≠ 0, then 1 + sec x + sec² x + sec³ x + sec⁴ x + sec⁵ x is equal to ……………
(1) (1 + sec x) (sec² x + sec³ x + sec⁴ x)
(2) (1 + sec x) (1 + sec² x + sec⁴ x)
(3) (1 – sec x) (sec x + sec³ x + sec⁵ x)
(4) (1 + sec x) (1 + sec³ x + sec⁴ x)
Answer:
(2) (1 + sec x) (1 + sec² x + sec⁴ x).
Hint:
1 + sec x + sec² x + sec³ x
+ sec⁴ x + sec⁵ x
= (1 + sex x) + sec² x (1 + sec x) + sec⁴ x (1 + see x)
= (1 + sec x) + sec² x (1 + sec x) + sec⁴ x (1 + secx)
= (1 + sec x) (1 + sec² x + sec⁴ x)

Question 23.
If the n^th term of an A.P. is t_n = 3 – 5n, then the sum of the first n terms is …………….
(1) \(\frac { n }{ 2 } \) [1 – 5n]
(2) n (1 – 5n)
(3) \(\frac { n }{ 2 } \) (1 + 5n)
(4) \(\frac { n }{ 2 } \) (1 + n)
Answer:
(1) \(\frac { n }{ 2 } \) [1 – 5n]
Hint:
t_n =. 3 – 5(n)
t₁ = 3 – 5(1) = -2 ; t₂ = 3 – 10 = -7
a = -2, d = -7 – (-2) = -5
S_n = \(\frac { n }{ 2 } \) [2a + (n – 1)d]
= \(\frac { n }{ 2 } \) [-4 + (n – 1) (-5)]
= \(\frac { n }{ 2 } \) [- 4 -5n + 5] = \(\frac { n }{ 2 } \) [1 – 5n]

Question 24.
The common ratio of the G.P. a^m-n, a^m, a^m+n is …………
(1) a^m
(2) a^-m
(3) aⁿ
(4) a^-n
Answer:
(3) aⁿ

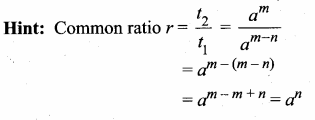
Question 25.
If 1 + 2 + 3 + … + n = k then 1³ + 2³ + ……. + n³ is equal to …………
(1) K²
(2) K³
(3) \(\frac{k(k+1)}{2}\)
(4) (K + 1)³
Answer:
(1) K²

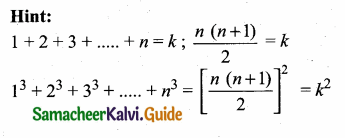
II. Answer the following.

Question 1.
Show that the square of any positive integer of the form 3m or 3m + 1 for some integer m.
Answer:
Let a be any positive integer. Then it is of the form 3q or 3q + 1 or 3q + 2
Case – 1 When a = 3q
a² = (3q)² = 9 q²
= (3q) (3q)
= 3m where m = 3q
Case – 2 When a = 3q + 1
a² = (3q + 1)² = 9q² + 6q + 1
= 3q (3q + 2) + 1
= 3 m + 1
where m = q (3q + 2)
Case – 3 When a = 3q + 2
a² = (3q + 2)² = 9q² + 12q + 4
= 9q² + 12q + 3 + 1
= 3(3q² + 4q + 1) + 1
= 3m + 1
where m = 3q² + 4q + 1
Hence a is of the form 3m or 3m + 1

Question 2.
Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is some integer.
Solution:
Let us start with taking a, where a is a +ve odd integer.
We apply the division algorithm with ‘a’ and ‘b’ = 4.
Since 0 < r < 4, the possible remainders are 0, 1, 2, 3.
That is, a can be 4q, or 4q + 1, or 4q + 2 or 4q + 3, where 1 is the quotient. However, since a is odd, a cannot be 4q or 4q + 2 (since they are both divisible by 2).
Any odd integer is of the form 4q + 1 or 4q + 3.

Question 3.
Compute x such that 5⁴ = x (mod 8)
Answer:
5² = 25 = 1 (mod 8)
5⁴ = (5²)² = l² (mod 8)
= 1
5⁴ = 1 (mod 8)

Question 4.
The first term of an A.P. is 6 and the common difference is 5. Find the A.P. and its general term.
Answer:
Given, a = 6, d = 5
General term t_n = a + (n – 1) d
= 6 + (n – 1) 5
= 6 + 5 n – 5
= 5 n + 1
The general form of the A.P. is a, a + d, a + 2d,
The A.P. is 6, 11, 16, 21, ……… 5n + 1.

Question 5.
Which term of the arithmetic sequence 24, 23\(\frac { 1 }{ 4 } \), 22 \(\frac { 1 }{ 2 } \), 21 \(\frac { 3 }{ 4 } \), …….. is 3?
Answer:
Given The A.P is 24, 23 \(\frac { 1 }{ 4 } \), 22 \(\frac { 1 }{ 2 } \), 21 \(\frac { 3 }{ 4 } \), …………..

Question 6.
Determine the AP whose 3rd term is 5 and the 7th term is 9.
Solution:
We have
a₃ = a + (3 – 1)d = a + 2d = 5 ……….. (1)
a₇ = a + (7 – 1)d = a + 6d = 9 ………… (2)
(1) – (2) ⇒ -4d = -4 ⇒ d = 1.
Sub, d = 1 in (1), we get
a + 2(1) = 5
a = 3
Hence the required A.P. is 3, 4, 5, 6, 7.

Question 7.
If a, b, c are in A.P. then prove that (a – c)² = 4 (b² – ac).
Answer:
Given a, b, c are in A.P.
n = 10
∴ b – a = c – b
2 b = a + c
Squaring on both sides,
(a + c)² = (2b)²
a² + c² + 2ac = 4b²
(a – c)² + 2ac + 2ac = 4b²
[a² + c² = (a – c)² + 2ac]
(a – c)² = 4b² – 4ac
(a – c)² = 4(b² – ac)
Hence it is proved.
Aliter: Given a, b, c are in A.P.
b – a = c – b
2b = a + c
To prove, (a – c)² = 4(b² – ac)
L.H.S.= (a – c)²
= a² + c² – 2 ac
= (a + c)² – 2 ac – 2ac
= (a + c)² – 4ac
= (2b)² – 4ac (2b = a + c)
= 4b² – 4ac = 4 (b² – ac) = R.H.S
∴ L.H.S = R.H.S., Hence proved.

Question 8.
If the sum of the first 14 terms of an AP is 1050 and its first term is 10, find the 20th term.
Solution:
Here S₁₄ = 1050
n = 14
a = 10
S_n = \(\frac { n }{ 2 } \) (2a + (n – 1)d)
1050 = \(\frac { 14 }{ 2 } \) (20 + 13d)
= 140 + 91d
910 = 91d
d = 10
a₂₀ = 10 + (20 – 1) × 10
= 20
∴ 20th term = 200.

Question 9.
Find the sum of the first 40 terms of the series 1² – 2² + 3² – 4² + ….
Answer:
The given series is 1² – 2² + 3² – 4² + …. 40 terms
Grouping the terms we get,
(1² – 2²) + (3² – 4²) + (5² – 6²) + ………….. 20 terms
(1 – 4) + (9 – 16) + (25 – 36) + …………… 20 terms
(- 3) + (- 7) + (- 11) + ………………. 20 term
This is an A.P
Here a = – 3, d = – 7 – (-3) = – 7 + 3 = – 4 n = 20
S_n = \(\frac { n }{ 2 } \) [2a + (n – 1) d ]
S₂₀ = \(\frac { 20 }{ 2 } \) [2(-3) + 19(-4)]
= 10 (- 6 – 76) = 10 (- 82) = – 820
∴ Sum of 40 terms of the series is – 820.
Aliter. 1² – 2² + 3² – 4² + …….. + 39² – 40²
= 1² + 3² + 5² + ……. + 39² –
(2² + 4² + 6² + ……….. + 40²)
= 1² + 2² + 3² + 4² + …. + 40²
– (2² + 4² + 6² + …. + 40²)
– (2² + 4² + 6² + …. + 40²)
= 1² + 2² + 3² + …. + 40²
= 2 × 2² (1² + 2² + ….. + 20²)

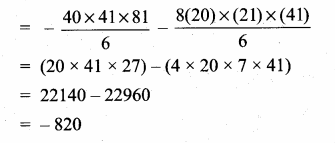
Question 10.
Find the sum of first 24 terms of the list of numbers whose nth term is given by
a_n = 3 + 2n.
Solution:
a_n = 3 + 2n
a₁ = 3 + 2 = 5
a₂ = 3 + 2 × 2 = 7
a₃ = 3 + 2 × 3 = 9
List of numbers becomes 5, 7, 9. 11, ……….
Here,7 – 5 = 9 – 7 = 11 – 9 = 2 and soon. So, it forms an A.P. with common difference d = 2.
To find S₂₄, we have n = 24, a = 5, d = 2.
S₂₄ = \(\frac { 24 }{ 2 } \) [2 × 5 + (24 – 1) × 2 ]
= 12 [10 + 46] = 672
So, sum of first 24 terms of the list of numbers is 672.

Question 11.
If a clock strikes once at 1 o’clock, twice at 2 o’clock and so on, how many times will it strike in a day?
Answer:
Number of times the clock strikes each hour form an A.P.
Number of times strike in 12 hours is
1 + 2 + 3 + …….. + 12
Here, a = 1, d = 1, n = 12, l = 12
S_n = \(\frac { n }{ 2 } \) (a + l) = \(\frac { 12 }{ 2 } \) (1 + 12)
= 6 × 13 = 78 times
∴ Number of times the clock strike in 24 hours
= 78 × 2 = 156 times.

Question 12.
If the 4^th and 7^th terms of a G.P. are 54 and 1458 respectively, find the G.P.
Answer:
Given, t₄ = 54 and t₇ = 1458

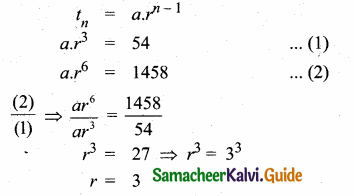
Substituting the value of r = 3 in (1)
a × 27 = 54
a = \(\frac { 54 }{ 27 } \) = 2
∴ The Geometric sequence is 2, 6, 18, 54 ………

Question 13.
Which term of the geometric sequence,
(i) 5, 2, \(\frac { 4 }{ 5 } \), \(\frac { 8 }{ 25 } \), ……… is \(\frac { 128 }{ 15625 } \)?
Answer:
The given G.P. is 5, 2, \(\frac { 4 }{ 5 } \),\(\frac { 8 }{ 25 } \), …….., is \(\frac { 128 }{ 15625 } \)
Here a = 5, r = \(\frac { 2 }{ 5 } \), t_n = \(\frac { 128 }{ 15625 } \)
t_n = a.r^n-1

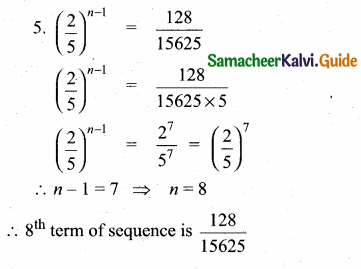
Question 14.
How many consecutive terms starting from the first term of the series 2 + 6 + 18 + … would sum to 728?
Answer:
The given series is
2 + 6 + 18 + …. + t_n = 728
Here a = 2, r = = 3, S_n = 728

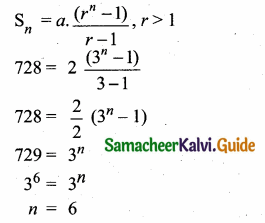
∴ Required number of terms = 6

Question 15.
A geometric series consists of four terms and has a positive common ratio. The sum of the first two terms is 9 and sum of the last two terms is 36. Find the series.
Answer:
Let the four terms of the G.P. be a, ar, ar² and ar³ ……….
Given, a + ar = 9 ……(1)
ar² + ar³ = 36
r² (a + ar) = 36
r² (9) = 36
[from (1)]
r² = =4
r = ± 2
then r = 2
(given common positive ratio)
a + a (2) = 9 from (1)
3a = 9
a = 3
∴ The required series
= 3 + 3(2) + 3 (2²) + 3 (2³) + ……
= 3 + 6 + 12 + 24 + ……..

Question 16.
Suppose that five people are ill during the first week of an epidemic and each sick person spreads the contagious disease to four other people by the end of the second week and so on. By the end of 15^th week, how many people will be affected by the epidemic?
Answer:
Number of people affected by the epidemic during each week form a geometric series.
S₁₅ = 5 + (4 × 5) + (4 × 20) + (4 × 80) + …. 15 terms
= 5 + 20 + 80 + 320 + … 15 terms
Here a = 5, r = 4, n = 15

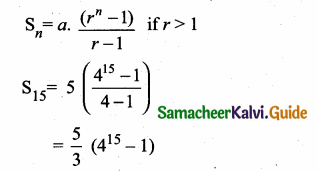
Question 17.
A gardener wanted to reward a boy for his good deeds by giving some mangoes. He gave the boy two choices. He could either have 1000 mangoes at once or he could get 1 mango on the first day, 2 on the second day, 4 on the third day, 8 mangoes on the fourth day and so on for ten days. Which option should the boy choose to get the maximum number of mangoes?
Answer:
I choice
The boy could get 1000 mangoes at once
II choice
The boy receives mangoes daily for ten days
S₁₀ = 1 + 2 + 4 + 8 + ……… 10 terms

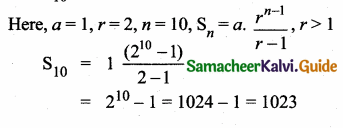
Question 18.
Find the value of k if
1³ + 2³ + 3³ + ….. + K³ = 2025
Answer:
Given, 1³ + 2³ + 3³ + … + K³ = 2025

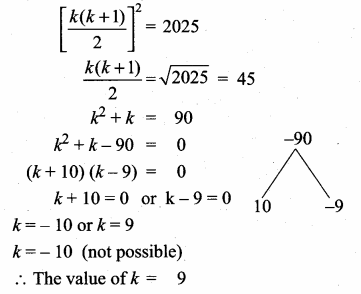
Question 19.
If 1³ + 2³ + 3³ + …… + K³ = 8281, then find 1 + 2 + 3 + … + K.
Answer:
Given, 1³ + 2³ + 3³ + …… + K³ = 8281

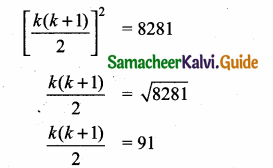
1 + 2 + 3 + …… + K = 91

Question 20.
Find the sum of all 11 term of an AP whose middle most term in 30.
Answer:
Let ‘a’ be the first term and ‘d’ be the common difference of the give A.P.
Middle most term = (\(\frac { 11+1 }{ 2 } \))^th = 6^th term
t_n = a + (n – 1)d
t₆ = a + 5d
a + 5d = 30
S_n = \(\frac { n }{ 2 } \) [2a + (n – 1)d]
S₁₁ = \(\frac { 11 }{ 2 } \) [2a + 10d]
= \(\frac { 11 }{ 2 } \) × 2 [a + 5d]
= 11 × 30
= 330
Sum of 11 terms = 330

III. Answer the following.

Question 1.
Use Euclid’s division algorithm to find the HCF of 867 and 255.
Answer:
Here 867 > 255
Applying Euclid’s Lemma to 867 and 255 we get

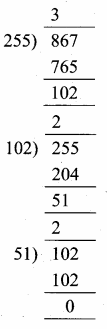
867 = (255 × 3) + 102
The remainder 102 ≠ 0
Again applying Euclid’s
Lemma to 255 and 102
255 = 102 × 2 + 51
The remainder 51 ≠ 0
Again applying Euclid’s
Lemma to 102 and 51 we get
102 = 51 × 2 + 0
The remainder is 0
∴ HCF of 867 and 255 is 51

Question 2.
Find the number of integer solutions of 5x = 2 (mod 13)
Answer:
5x ≡ 2 (mod 13) can be written as
5x – 2 = 13 k for some integer
5x = 13 k + 2
x = \(\frac{13 k+2}{5}\)
Since 5k is an integer \(\frac{13 k+2}{5}\) cannot be an inter.
There is no integer solution.

Question 3.
Find the 40^th term of A.P. whose 9^th term is 465 and 20^th term is 388.
Answer:
t_n = a + (n – 1) d
t₉ = a + 8d (t₉ = 465)
a + 8d = 465 ……(1)

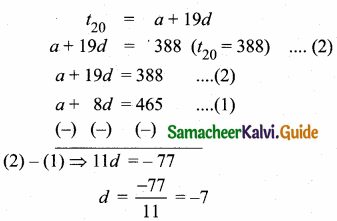
Substitute the value of d = -7 in (1)
a + 8(-7) = 465
a – 56 = 465
a = 465 + 56 = 521
a = 521, d = -7, n = 40
t₄₀ = 521 + 39(-7)
= 521 – 273
= 248
40^th term of an A.P. is 248

Question 4.
Find the three consecutive terms in an A.P. whose sum is 18 and the sum of their squares is 140.
Answer:
Let the three consecutive terms in an
A.P. be m – d,m,m + d
By the given data,
Sum of threee terms = 18
m – d + m + m + d = 18
3m = 18
m = \(\frac { 18 }{ 3 } \) = 6
Again by the given data,
Sum of their squares = 140
(m – d)² + m² + (m + d)² = 140
m² + d² – 2md + m² + m² + d² + 2md = 140
3m² + 2d² = 140
3(62) + 2d² = 140
3(36) + 2d² = 140
2d² = 140 – 108
2d² = 32
d² = \(\frac { 32 }{ 2 } \) = 16
∴ d = ± 4
when, m = 6, d = + 4
m – d = 6 – 4 = 2
m = 6
m + d = 6 + 4 = 10
when, m = 6, d = -4
m – d = 6-(-4) = 6 + 4= 10
m = 6
m + d = 6 +(-4) = 6 – 4 = 2
∴ The three numbers are 2, 6 and 10 or 10, 6,2.

Question 5.
If m times the m^th term of an A.P. is equal to n times its n^th term, then show that the (m + n)^th term of the A.P. is zero.
Answer:
Given, mt_m = nt_n
m[a + (m – 1) d] = n [a + (n – 1) d]
[we know that t_n = a + (n – 1)d]
m[a + md – d] = n[a + nd – d]
ma + m²d – md = na + n²d – nd
ma – na + m²d – n²d = md – nd
a (m – n) + d (m² – n²) = d(m – n)
a (m – n) + d(m + n)(m – n) = d(m – n) ÷ by (m – n) on both sides,
a + d (m + n) = d
a + d(m + n) – d = 0
a + d(m + n – 1) = 0 ….. (1)
To prove, t_(m+n) = 0
t_(m+n) = a + (m + n – 1)d
t_(m+n) = 0(from(1))
Hence it is proved.

Question 6.
If a, b, c are in A.P. then prove that (a – c)² = 4 (b² – ac).
Answer:
Given a, b, c are in A.P.
∴ b – a = c – b
2 b = a + c
Squaring on both sides,
(a + c)² = (2b)²
a² + c² + 2 ac = 4 b²
(a – c)² + 2 ac + 2 ac = 4 b²
[a² + c² = (a – c)² + 2 ac]
(a – c)² = 4b² – 4ac
(a – c)² = 4 (b² – ac)
Hence it is proved.
Aliter: Given a, b, c are in A.P.
b – a = c – b
2 b = a + c
To prove, (a – c)² = 4(b² – ac)
L.H.S. = (a – c)²
= a² + c² – 2ab
= (a + c)² – 2ac – 2ac
= (a + c)² – 4ac
= (2b)² – 4ac (2b = a + c)
= 4 b² – 4ac = 4 (b² – ac) = R.H.S
∴ L.H.S = R.H.S., Hence proved.

Question 7.
The ratio of the sums of first m and first n terms of an arithmetic series is m² : n² show that the ratio of the m^th and n^th terms is (2m – 1) : (2n -1).
Answer:

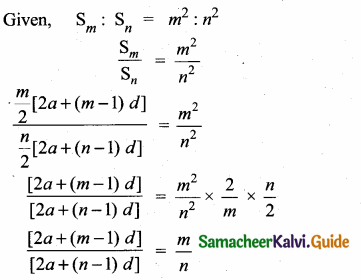
n[2a + (m – 1) d] = tn[2a + nd-d]
2 an + mnd- nd = 2 am + mnd— md 2an-2am = nd- md 2 a (n-m) = d(n- m)
÷ by (n – m) on both sides,
2a = d
To prove, t_m : t_n = (2m – 1) : (2n – 1)
L.H.S = t_m : t_n
= a + (m – 1) d : a + (n – 1)d
= a + (m – 1) 2a : a + (n – 1)2a
[Substitute the value of d = 2a]
= a + 2 am – 2 a: a + 2 am – 2a
= 2am – a : 2an – a
= a (2m – 1) : a (2n – 1)
= (2m – 1) : (2n – 1) = R. H. S
= (2m – 1) : (2n – 1)
∴ t_m : t_n
L.H.S = R.H.S
Hence it is proved.

Question 8.
A construction company will be penalised each day for delay in construction of a bridge. The penalty will be ₹4000 for the first day and will increase by ₹1000 for each following day. Based on its budget, the company can afford to pay a maximum of ₹1,65,000 towards penalty. Find the maximum number of days by which the completion of work can be delayed.
Solution:
Penalty for the first day (a) = ₹ 4000
Increased rate for every day (d) = ₹ 1000
Maximum amount of penalty (S_n)
= ₹ 1,65,000
S_n = \(\frac { n }{ 2 } \) [2a + (n-1) 1000]
165000 = \(\frac { n }{ 2 } \) [2(4000) + (n – 1) 1000]
= \(\frac { n }{ 2 } \) [8000 + 1000 n – 1000]
165000 = \(\frac { n }{ 2 } \) (7000 + 1000n)
330000 = 7000 n + 1000 n²
0 = 1000 n² + 7000 n – 330000 ÷ 1000 on both sides,
n² + 7n – 330 = 0
(n + 22) (n – 15) = 0
n = -22 or n = 15
n = -22 (not possible)
∴ Maximum number of days for which the work can be delayed is 15 days.

Question 9.
If the product of three consecutive terms in G.P. is 216 and sum of their products in pairs is 156, find them.
Let the three consecutive terms of G.P. be \(\frac { a }{ r } \), a, ar.
Product of three terms = 216
\(\frac { a }{ r } \) × a × ar = 216
a³ = 216
a³ = 63
a = 6
Sum of their products in pairs = 156

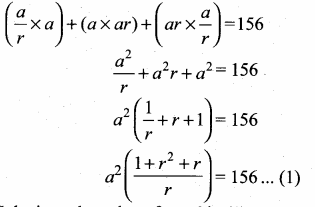
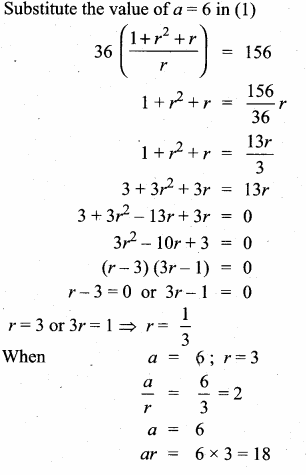
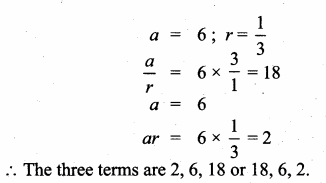
Question 10.
If a, b, c, d are in a geometric sequence, then show that
(a – b + c) (b + c + d) = ab + bc + cd.
Answer:
Given, a, b, c, d are in a geometric sequence.
Let a = a, b = ar, c = ar², d = ar³
To prove, (a – b + c) (b + c + d) = ab + bc + cd
L.H.S. = (a – b + c)(b + c + d)
= (a – ar + ar²) (ar + ar² + ar³ )
= a (1 – r + r²)ar (1 + r + r²)
= a²r (1 – r + r²) (1 + r + r²)
= a²r (1 + r² + r4)
= a²r + a²r³ + a²r⁵
= a (ar) + ar (ar²) + ar² (ar³)
= ab + bc + cd
= R.H.S.
L.H.S. = R.H.S., Hence proved.

Question 11.
Find the sum of the first n terms of the series 0.4 + 0.94 + 0.994 + ………..
Answer:
Given series is 0.4 + 0.94 + 0.994 + ……………. + n terms.
S_n = 0.4 + 0.94 + 0.994 + ……….. + n terms

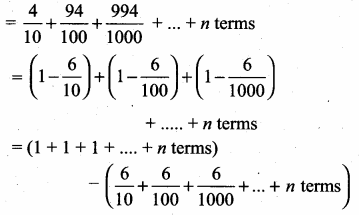
Question 12.
Find the total area of 12 squares whose sides are 12 cm, 13 cm,… 23 cm respectively.
Answer:
Given, the sides of 12 squares are 12 cm, 13 cm, 14 cm,… 23 cm
Total area of 12 squares
= 12² + 13² + 14² + … + 23²
= (1² + 2² + 3² … + 23²) – (1² + 2² + … + 11²)