Students can download Maths Chapter 1 Relations and Functions Ex 1.4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Ex 1.4
Question 1.
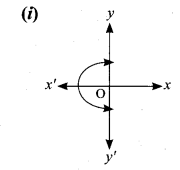
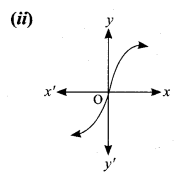
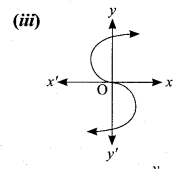
Determine whether the graph given below represent functions. Give reason for your answers concerning each graph.
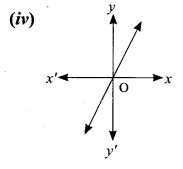
Answer:
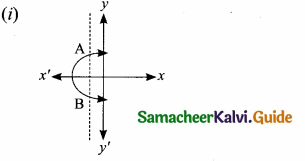
The vertical line cuts the graph at A and B. The given graph does not represent a function.
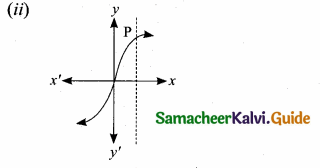
![]()
The vertical line cuts the graph at most one point P. The given graph represent a function.
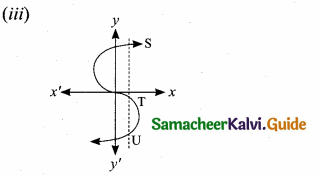
The vertical line cuts the graph at three points S,T and U. The given graph does not represent a function.
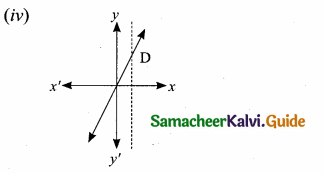
The vertical line cuts the graph at most one point D. The given graph represents a function.
Question 2.
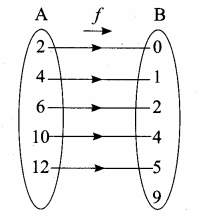
Let f: A → B be a function defined by
f(x) = \(\frac { x }{ 2 } \) – 1, where A = {2, 4,6,10,12},
B = {0,1,2,4,5,9}. Represent f by
(i) set of ordered pairs
(ii) a table
(iii) an arrow diagram
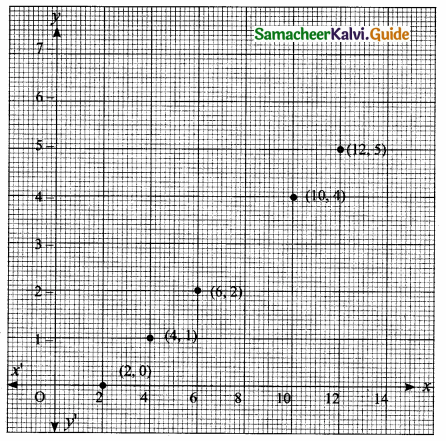
(iv) a graph
Answer:
A = {2,4,6, 10, 12}
B = {0,1, 2, 4, 5, 9}
f(x) = \(\frac { x }{ 2 } \) – 1
f(2) = \(\frac { 2 }{ 2 } \) – 1 = 1 – 1 = 0
f(4) = \(\frac { 4 }{ 2 } \) – 1 = 2 – 1 = 1
f(6) = \(\frac { 6 }{ 2 } \) – 1 = 3 – 1 = 2
f(10) = \(\frac { 10 }{ 2 } \) – 1 = 5 – 1 = 4
f(12) = \(\frac { 12 }{ 2 } \) – 1 = 6 – 1 = 5
![]()
(i) Set of ordered pairs
f = {(2, 0) (4, 1) (6, 2) (10, 4) (12, 5}
(ii) Table
| X | 2 | 4 | 6 | 10 | 12 |
| f(x) | 0 | 1 | 2 | 4 | 5 |
(iii) Arrow diagram
(iv) Graph
![]()
Question 3.
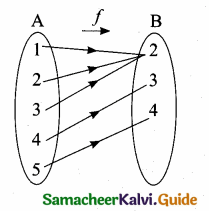
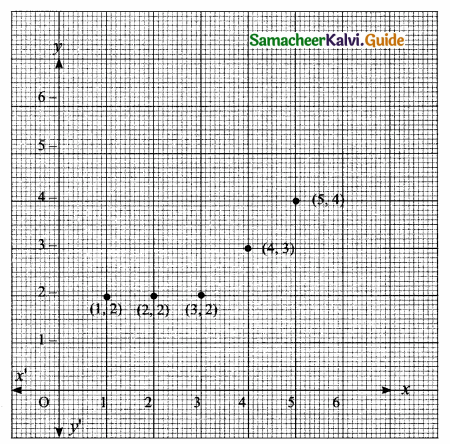
Represent the function f = {(1,2), (2,2), (3,2), (4,3),(5,4)} through (i) an arrow diagram (it) a table form (iii) a graph.
Answer:
f = {(1, 2) (2, 2) (3, 2) (4, 3) (5,4)}
Let A = {1,2, 3, 4, 5}
B = {2, 3, 4}
(i) Arrow diagram
(ii) Table form
| X | 1 | 2 | 3 | 4 | 5 |
| f(x) | 2 | 2 | 2 | 3 | 4 |
(iii) Graph
![]()
Question 4.
Show that the function f : N → N defined by f(x) = 2x – 1 is one-one but not onto.
Answer:
f: N → N
N = {1,2,3,4,5,… }
f(x) = 2x – 1
f(1) = 2(1) – 1 = 2 – 1 = 1
f(2) = 2(2) – 1 = 4 – 1 = 3
f(3) = 2(3) – 1 = 6 – 1 = 5
f(4) = 2(4) – 1 = 8 – 1 = 7
f(5) = 2(5) – 1 = 10 – 1 = 9
f = {(1,1) (2, 3) (3, 5) (4, 7) (5,9) …..}
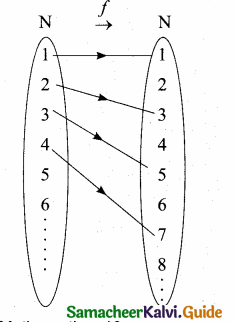
(i) Different elements has different images. This function is one to one function.
(ii) Here Range is not equal to co-domain. This function not an onto function.
∴ The given function is one-one but not an onto.
![]()
Question 5.
Show that the function f: N ⇒ N defined by f(m) = m2 + m + 3 is one-one function.
Answer:
N = {1,2,3, 4,5, ….. }
f(m) = m2 + m + 3
f(1) = 12 + 1 + 3 = 5
f(2) = 22 + 2 + 3 = 9
f(3) = 32 + 3 + 3 = 15
f(4) = 42 + 4 + 3 = 23
f = {(1,5) (2, 9) (3, 15) (4, 23)}
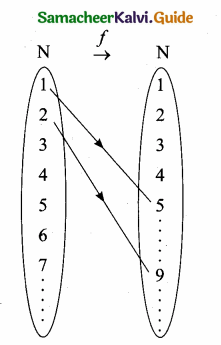
From the diagram we can understand different elements in (N) in the domain, there are different images in (N) co-domain.
∴ The function is a one-one function.
Question 6.
Let A = {1, 2, 3, 4) and B = N. Letf: A → B be
defined by f(x) = x3 then,
(i) find the range off
(ii) identify the tpe of function
Solution:
A = {1, 2, 3, 4}
B = N
f: A → B,f(x) = x3
(i) f(1) = 13 = 1
f(2) = 23 = 8
f(3) = 33 = 27
f(4) = 43 = 64
(ii) Therange of f = {1, 8, 27, 64 )
(iii) It is one-one and into function.
![]()
Question 7.
In each of the following cases state whether the function is bijective or not. Justify your answer.
(i) f: R → R defined by f (x) = 2x + 1
(ii) f: R → R defined by f(x) = 3 – 4x2
Answer:
(i) f(x) = 2x + 1
f(0) = 2(0) + 1 = 0 + 1 = 1
f(1) = 2(1) + 1 = 2 + 1 = 3
f(2) = 2(2) + 1 = 4 + 1 = 5
f(3) = 2(3) + 1 = 6 + 1 = 7
Different elements has different images
∴ It is an one-one function.
It is also an onto function. The function is one-one and onto function.
∴ It is a bijective function.
(ii) f(x) = 3 – 4x2
f(1) = 3 – 4(1)2
= 3 – 4 = -1
f(2) = 3 – 4(2)2 = 3 – 16 = – 13
f(3) = 3 – 4(3)2 = 3 – 36 = – 33
f(4) = 3 – 4(42) = 3 – 64 = – 61
It is not a bijective function. The positive numbers “R” do not have negative pre – image in X in R.
![]()
Question 8.
Let A= {-1,1}and B = {0,2}.
If the function f: A → B defined by
f(x) = ax + b is an onto function? Find a and b.
Answer:
A = {-1, 1}; B = {0,2}
f(x) = ax + b
f(-1) = a(-1) + b
0 = -a + b
a – b = 0 ….(1)
f(1) = a(1) + b
2 = a + b
a + b = 2 ….(2)
Solving (1) and (2) we get
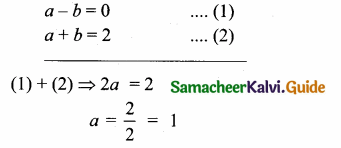
Substitute a = 1 in (1)
The value of a = 1 and b = 1
Question 9.
If the function f is defined by
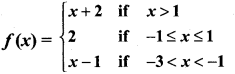
find the value of
(i) f(3)
(ii) f(0)
(iii) f(1. 5)
(iv) f(2) + f(-2)
Answer:
f(x) = x + 2 when x = {2,3,4,……}
f(x) = 2
f(x) = x – 1 when x = {-2}
(i) f(x) = x + 2
f(3) = 3 + 2 = 5
(ii) f(x) = 2
f(0) = 2
(iii) f(x) = x – 1
f(-1.5) = -1.5 – 1 = -2.5
(iv) f(x) = x + 2
f(2) = 2 + 2 = 4
f(x) = x – 1
f(-2) = – 2 – 1 = – 3
f(2) + f(-2) = 4 – 3
= 1
![]()
Question 10.
A function f: [-5, 9] → R is defined as follows:
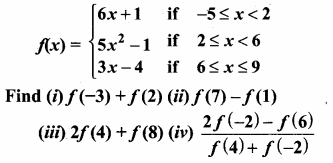
Answer:
f(x) = 6x + 1 ; x = {-5,-4,-3,-2,-1,0,1}
f(x) = 5x2 – 1 ; x = {2, 3, 4, 5}
f(x) = 3x – 4 ; x = {6, 7, 8, 9}
(i) f(-3) + f(2)
f(x) = 6x + 1
f(-3) = 6(-3) + 1 = -18 + 1 = -17
f(x) = 5x2 – 1
f(2) = 5(2)2 – 1 = 20 – 1 = + 19
f(-3) + f(2) = – 17 + 19
= 2
(ii) f(7) – f(1)
f(x) = 3x – 4
f(7) = 3(7) – 4 = 21 – 4 = 17
f(x) = 6x + 1
f(1) = 6(1) + 1 = 6 + 1 = 7
f(7) – f(1) = 17 – 7
= 10
(iii) 2f(4) + f(8)
f(x) = 5x2 – 1
f(4) = 5(4)2 – 1 = 5(16) – 1
= 80 – 1 = 79
f(x) = 3x – 4
f(8) = 3(8) – 4 = 24 – 4 = 20
2f(4) + f(8) = 2(79) + 20
= 158 + 20
= 178
![]()
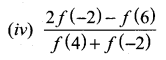
f(x) = 6x + 1
f(-2) = 6(-2) + 1 = -12 + 1 = -11
f(x) = 3x – 4
f(6) = 3(6) – 4 = 18 – 4 = 14
f(x) = 5x2 – 1
f(4) = 5(4)2 – 1 = 5(16) – 1
= 80 – 1 = 79
f(x) = 6x + 1
f(-2) = 6(-2) + 1 = -12 + 1 = -11
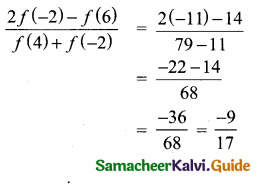
Question 11.
The distance S an object travels under the influence of gravity in time t seconds is given by S(t) = \(\frac{1}{2}\) gt2 + at + b where, (g is the acceleration due to gravity), a, b are constants. Check if the function S (t)is one-one.
Solution:
S(t) = \(\frac{1}{2}\) gt2 + at + b
Let t be 1, 2, 3, ………, seconds
S(1) = \(\frac{1}{2}\) g(12) + a(1) + b = \(\frac{1}{2}\) g + a + b
S(2) = \(\frac{1}{2}\) g(22) + a(2) + b = 2g + 2a + b
Yes, for every different values of t, there will be different values as images. And there will be different preimages for the different values of the range. Therefore it is one-one function.
![]()
Question 12.
The function ‘t’ which maps temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by
t(C) = F where F = \(\frac { 9 }{ 5 } \) C + 32. Find,
(i) t(0)
(ii) t(28)
(iii) t(-10)
(iv) the value of C when t(C) = 212
(v) the temperature when the Celsius value is equal to the Fahrenheit value.
Answer:
Given t(C) = \(\frac { 9C }{ 5 } \) + 32
(i) t(0) = \(\frac { 9(0) }{ 5 } \) + 32
= 32° F
(ii) t(28) = \(\frac { 9(28) }{ 5 } \) + 32
= \(\frac { 252 }{ 5 } \) + 32
= 50.4 + 32
= 82.4° F
(iii) t(-10) = \(\frac { 9(-10) }{ 5 } \) + 32
= -18 + 32
= 14° F
(iv) t(C) = 212
\(\frac { 9C }{ 5 } \) + 32 = 212
\(\frac { 9C }{ 5 } \) = 212 – 32
= 180
9C = 180 × 5
C = \(\frac{180 \times 5}{9}\)
= 100° C
(v) consider the value of C be “x”
t(C) = \(\frac { 9C }{ 5 } \) + 32
x = \(\frac { 9x }{ 5 } \) + 32
5x = 9x + 160
-160 = 9x – 5x
-160 = 4x
x = \(\frac { -160 }{ 4 } \) = -40
The temperature when the Celsius value is equal to the fahrenheit value is -40°
![]()
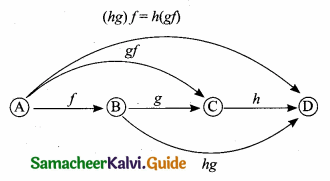
Composition of two Functions
Let f: A → B and g: B → C be two functions. Then the composition of f and g denoted by gof is defined as the function gof (x) = g[f(x)] for all x ∈ A.
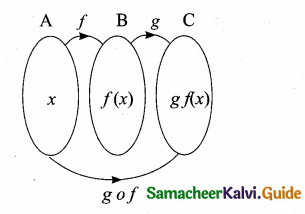
Composition of three Functions
Let A, B, C, D be four sets and let f: A → B; g : B → C and h : C → D be three functions, using composite functions fog and goh, we get two new functions like (fog) oh and fo (goh).
Note: Composition of three function is always associative.