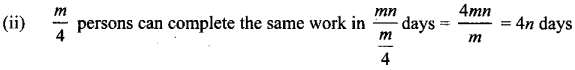Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 4 Life Mathematics InText Questions Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 4 Life Mathematics InText Questions
Try These (Text Book Page No. 122)
Find the indicated percentage value of the given numbers.
Answer:

![]()
Try These (Text Book Page No. 124)
Question 1.
What percentage ola day is 10 hours?
Answer:
In a day, there are 24 hours .
∴ 10 hrs out of 24 hrs is \(\frac{10}{24}\)
As a percentage, we need to multiply by 100
∴ Percentage = \(\frac{10}{24}\) × 100 = 41.67%
Question 2.
Divide ₹ 350 among P, Q and R such that P gets 50% of what Q gets and Q gets 50% of what R gets.
Answer:
Let R get x, Q gets 50% of what R gets
∴ Q gets = \(\frac{50}{100} \times x=\frac{x}{2}\)
P gets 50% of what Q gets .
∴ P gets = \(\frac{50}{100} \times \frac{x}{2}=\frac{x}{4}\)
Since 350 is divided among the three
∴ 350 = \(x+\frac{x}{2}+\frac{x}{4}\)
350 = \(\frac{4 x+2 x+x}{4}=\frac{7 x}{4}\) = 350
x = \(\frac{350 \times 4}{7}\)
Q gets = \(\frac{x}{2}=\frac{200}{2}\) = 100,
P gets = \(\frac{x}{4}=\frac{200}{4}\) = 50
∴ p = 50, Q = 100, R = 200
![]()
Think (Text Book Page No. 124)
With a lot of pride, the traffic police commissioner of a city reported that the accidents had decreased by 200% in one year. He came up with this number by stating that the increase in accidents from 200 to 600 is clearly a 200% rise and now that it had gone down from 600 last year to 200 this year should be a 200% fall. Is this decrease from 600 to 200, the same 200% as reported by him? Justify.

Answer:
Increase from original value 200 to 600
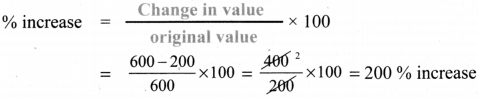
Decrease from original value 600 to 200
![]()
here original value is 600
% decrease = \(\frac{600-200}{600}\) × 100 = \(\frac{400}{600}\) × 100 = 66.67 % decrease
Increase from 200 → 600 and % decrease from 600 → 200 are not the same
![]()
Try These (Text Book Page No. 126)
Question 1.
If the selling price of an article is less than the cost price of the article, then there is a ________ .
Answer:
Loss
Question 2.
An article costing 5000 is sold for ₹ 4850. Is there a profit or loss? What percentage is it?
Answer:
Loss
Percentage of Loss

![]()
Question 3.
If the ratio of cost price and the selling price of an article is 5:7, then the profit / gain is ________ %.
Answer:
C.P = 5x
S.P = 7x
Profit = 7x – 5x = 2x
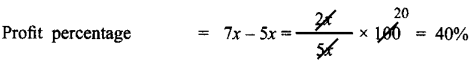
Think (Text Book Page No. 129)
A shopkeeper marks the price of a marker board 15% above the cost price and then allows a discount of 15% on the marked price. Does he gain or lose in the transaction?
Answer:
Let cost price of marker board be 100
CP = 100 Marks it 15% above CP
∴ Marked price MP = \(\frac{15}{100}\) × CP + CP
= \(\frac{15}{100}\) × 100 + 100 = 15 + 100 = 115
Discount % = 15 %
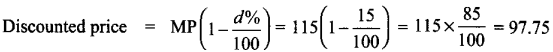
∴ He sells it 97.75 which is less than his cost price. Therefore he loses
Loss = 97.75 – 100 = – 2.25
![]()
Try These (Text Book Page No. 129)
Question 1.
The formula to find the simple interest for a given principal is ________ .
Answer:
\(\frac{\mathrm{PNR}}{100}\)
Question 2.
Find the simple interest on ₹ 900 for 73 days at 8% p.a.
Answer:
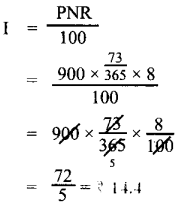
![]()
Question 3.
In how many years will ₹ 2000 become ₹ 3600 at 10% p.a simple interest?
Answer:
I = 3600 – 2000 = 1600
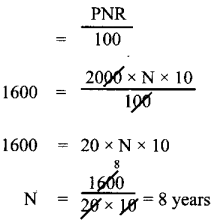
Try These (Text Book Page No. 141)
Question 1.
Classify the given examples as direct or inverse proportion:
(i) Weight of pulses to their cost.
Answer:
As weight increases cost also increases.
∴ Weight and cost are direct proportion.
(ii) Distance travelled by bus to the price of ticket.
Answer:
As the distance increases price to travel also increases,
∴ Distance and price are direct proportion.
![]()
(iii) Speed of the athelete to cover a certain distance.
Answer:
As the speed increases, the time to cover the distance become less.
So speed and üme are in indirect proportion.
(iv) Number of workers employed to complete a construction in a specified time.
Answer:
As the number of workers increases, the amount of work become less, so they are in indirect proportion.
(v) Area of a circle to its radius.
Answer:
If the radius of the circle increases its area also increases.
∴ Area and radius of circles are direct proportion.
![]()
Question 2.
A student can type 21 pages in 15 minutes. At the same rate, how long will it take student to type 84 pages?
Answer:
Direct proportion
No. of minutes = x
k = \(\frac{21}{15}\)
\(\frac{21}{15}=\frac{84}{x}\)
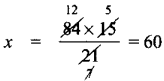
Question 3.
If 35 women can do a piece of work in 16 days, In how many days will 28 women do the same work?
Answer:
Inverse proportion
No. of days = x
k = 35 × 16
∴ 28 × x = 35 × 16
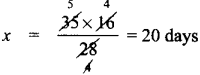
![]()
Try These (Text Book Page No. 145)
Question 1.
If x and y vary directly, find k when x = y = 5.
Answer:
I If x andy vary directly then \(\frac{x}{y}\) = k.
Here x = 5; y = 5
∴ k = \(\frac{5}{5}\)
k = 1
Question 2.
If x and y vary inversely, find the constant of proportionality when x = 64 and y = 0.75
Answer:
Gìven x = 64, y = 0.75
and also given x andy vary inversely.
∴ xy = k. the constant of variation.
∴ Constant = 64 × 0.75
Constant of variation = 48
![]()
Activity (Text Book Page No. 145)
Draw a circle of a given radius. Then, draw its radii in such a way that the angles between any two consecutive pair of radii are equal. Start drawing 3 radii and end with drawing 12 radii in the circle. List and prepare a table for the number of radii to the angle between a pair of consecutive radii and check whether they are in inverse proportion. What is the proportionality constant?
Answer:

As the number of radii increases angle decreases.
Hence they are in inverse proportion
∴ xy = 4 proportional constant
3 × 120° = 360° = k = 360°
![]()
Try These (Text Book Page No. 147)
Identify the different variations present in the following questions:
Question 1.
24 men can make 48 articles in 12 days. Then, 6 men can make _____ articles in 6 days.
Answer:
Let the required no. of articles be x
| Men (P) | Days (D) | Articles (W) |
| 24 | 12 | 48 |
| 6 | 6 | x |
(i) Mens and days are Indirect variables.
(ii) Men and Articles are direct vanables
(iii) Days and articles are also direct variables using formula.
Let
P1 = 24
P2 = 6
D1 = 12
D2 = 6
W1 = 48
W1 = x
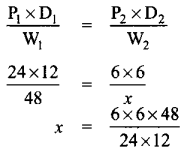
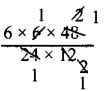
x = 6 Articles
![]()
Question 2.
15 workers can lay a road of length 4 km in 4 hours. Then, _____ workers can lay a road of length 8 km in 8 hours.
Answer:
Let the required no. of workers be x
| Length (work) | Hours | Workers |
| 4 km | 4 hrs | 15 |
| 8 km | 8 hrs | x |
(i) Length and workers are direct variable as more length need more workers.
The proportion is 4 : 8 : : 15 : x ——– (1)
(ü) Hours and workers are indirect variables as more working hours need less men.
∴ The proportion is : 4 : : 15 : x ——– (2)
Combining (1) and (2)
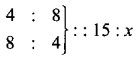
Product of the extremes = Product of the mean
4 × 8 × x = 8 × 4 × 15
x = \(\frac{8 \times 4 \times 15}{4 \times 8}\)
x = 15 workers
![]()
Question 3.
25 women working 12 hours a day can complete a work in 36 days. Then, 20 women must work hours a day to complete the same work in 30 days.
Answer:
Let the required hours be x.
| Women | Days | Hours |
| 25 | 36 | 12 |
| 20 | 30 | x |
As women increases hours to work decreases
∴ It is an inverse proportion.
∴ Multiplying factor is \(\frac{25}{20}\)
As days increases hours needed become less
∴ It is also an indirect variation.
∴ Multiplying factor is \(\frac{36}{30}\)
∴ x = \(12 \times \frac{25}{20} \times \frac{36}{30}\)
x = 18 hours
Question 4.
In a camp there are 420 kg of rice sufficient for 98 persons for 45 days. The number of days that 60 kg of rice will last for 42 persons is .
Answer:
Let the required number of days be x.
| Rice (kg) | Men | Days |
| 420 | 98 | 45 |
| 60 | 42 | x |
If amount of rice is more it will last for more days;
∴ It is Direct Proportion
∴ Multiplying factor is \(\frac{60}{420}\)
If men increases number of days the rice lasts decreases
∴ It is an inverse proportion.
∴ Multiplying factor is \(\frac{98}{42}\)
x = \(45 \times \frac{60}{420} \times \frac{98}{42}\)
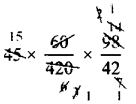
x = 15 days
![]()
Try These (Text Book Page No. 150)
Question 1.
Vikram can do one-third of work in p days. He can do th of work In ________ days.
Answer:
\(\frac{1}{3}\) of the work will be done mp days.
∴ Full work will be completed in 3p days
\(\frac{3}{4}\) th of the work will be done in = 3p x \(\frac{3}{4}\)
= \(\frac{9}{4}\)p = 2\(\frac{1}{4}\) p days.
Question 2.
If m persons can complete a work in n days, then 4m persons can complete the same
work in ______ days and \(\frac{m}{4}\) persons can complete the same work in ______ days.
Answer:
Givenm persons complete a work in n days
(i) Then work measured in terms of Man days = mn
4 m men do the work it will be completed in \(\frac{m n}{4 m}\) days = \(\frac{m}{4}\) days.