Samacheer Kalvi 8th Maths Guide Chapter 3 Algebra Ex 3.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.5

Question 1.
Subtract: -2(xy)² (y³ + 7x²y + 5) from 5y² (x²y³ – 2x⁴y + 10x²)
Answer:

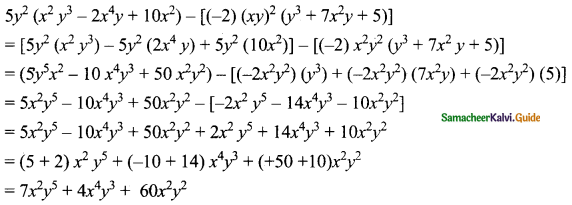
Question 2.
Multiply (4x² + 9) and (3x – 2).
Answer:
(4x² + 9)(3x – 2) = 4x²(3x – 2) + 9(3x – 2)
= (4x²)(3x) – (4x²) (2) + 9(3x) – 9(2)
= (4 × 3 × x × x²) – (4 × 2 × x²) + (9 × 3 × x) – 18
= 12x³ – 8x² + 27x – 18(4x³ + 9)(3x – 2)
= 12x³ – 8x² + 27x – 18

Question 3.
Find the simple interest on Rs. 5a²b² for 4ab years at 7b% per annum.
Answer:

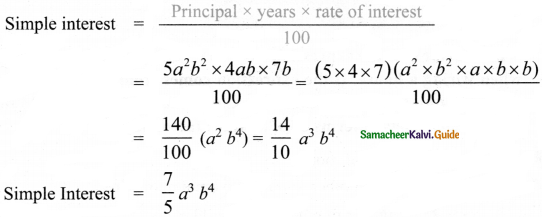
Question 4.
The cost of a note book is Rs. 10ab. If Babu has Rs. (5a²b + 20ab² + 40ab). Then how many note books can he buy?
Answer:
For ₹ 10 ab the number of note books can buy = 1.

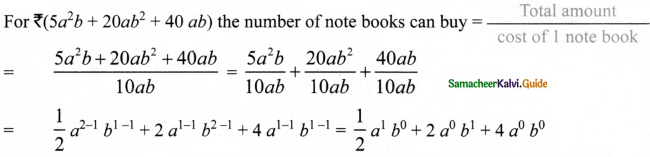
Number of note book he can buy = \(\frac { 1 }{ 2 }\)a + 2b + 4

Question 5.
Factorise: (7y² – 19y – 6)
Answer:
7y² – 19y – 6 is of the form ax² + bx + c where a = 7; b = – 19; c = – 6

Product = – 42	Sum = -19
1 × – 42 = -42	1 + (-42) = – 41
2 × – 21 = – 42	2 + (-21) = – 19

The product a × c = 7 × – 6 = – 42
sum b = – 19

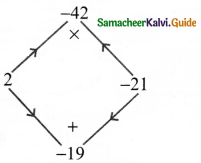
The middle term – 19 y can be written as – 21y + 2y
7y² – 19y – 6 = 7y² – 21y + 2y – 6
= 7y(y – 3) + 2(y – 3)
= (y – 3)(7y + 2)
7y² – 19y – 6 = (y – 3)(7y + 2)

Question 6.
A contractor uses the expression 4x² + 11x + 6 to determine the amount of wire to order when wiring a house. If the expression comes from multiplying the number of rooms times the number of outlets and he knows the number of rooms to be (x + 2), find the number of outlets in terms of ’x’. [Hint : factorise 4x² + 11x + 6]
Answer:
Given Number of rooms = x + 2
Number of rooms × Number of outlets = amount of wire.
(x + 2) × Number of outlets = 4x² + 11x + 6
Number of outlets = \(\frac{4 x^{2}+11 x+6}{x+2}\) … (1)
Now factorising 4x² + 11x + 6 which is of the form ax² + bx + c with a = 4 b = 11 c = 6.
The product a × c = 4 × 6 = 24
sum b = 11

Product = 24	Sum = 11
1 × 24 = 24	1 + 24 = 25
2 × 12 = 24	2 + 12 = 14
3 × 8 = 24	3 + 18 = 11

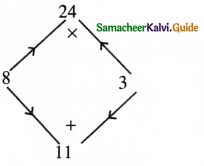
The middle term 11x can be written as 8x + 3x
∴ 4x² + 11 x + 6 = 4x² + 8x + 3x + 6
= 4x(x + 2) + 3 (x + 2)
4x² + 11x + 6 = (x + 2)(4x + 3)
Now from (1) the number of outlets

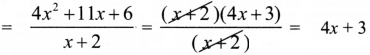
∴ Number of outlets = 4x + 3

Question 7.
A mason uses the expression x² + 6x + 8 to represent the area of the floor of a room. If the decides that the length of the room will be represented by (x + 4), what will the width of the room be in terms of x?
Answer:
Given length of the room = x + 4 .
Area of the room = x² + 6x + 8
Length × breadth = x² + 6x + 8
breadth = \(\frac{x^{2}+6 x+8}{x+4}\) ….. (1)
Factorizing x² + 6x + 8, it is in the form of ax² + bx + c
Where a =1 b = 6 c = 8.
The product a × c = 1 × 8 = 8
sum = b = 6

Product = 8	Sum = 6
1 × 8 = 8	1 + 8 = 9
2 × 4 = 8	2 + 4 = 6

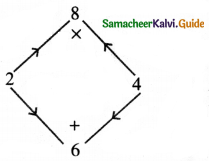
The middle term 6x can be written as 2x + 4x
∴ x² + 6x + 8 = x² + 2x + 4x + 8
= x(x + 2) + 4(x + 2)
x² + 6x + 8 = (x + 2)(x + 4)
Now from (1)

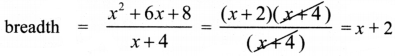
∴ Width of the room = x + 2

Question 8.
Find the missing term: y² + (-)x + 56 = (y + 7)(y + -)
Answer:
We have (x + a)(x + b) = x² + (a + b)x + ab
56 = 7 × 8
∴ y² + (7 + 8)x + 56 = (y + 7) (y + 8)

Question 9.
Factorise : 16p⁴ – 1
Answer:
16p⁴ – 1 = 2⁴p⁴ – 1 =(2²)² (p²)² – 1²
= (2²p²)² – 1²
Comparing with a² – b² (a + b)(a – b) where a = 2²p² and b= 1
∴ (2²p²)² – 1² = (2²p² + 1)(2²p² – 1)
= (4p² + 1)(4p² – 1)
∴ 16p⁴ – 1 = (4p² + 1)(4p² – 1) = (4p² + 1)(2²p² – 1²)
= (4p² + 1) [(2p)² – 1²] = (4p² + 1) (2p + 1)(2p – 1) [∵ using a² – b² = (a + b)(a – b)]
∴ 16p⁴ – 1 = (4p² + 1)(2p + 1)(2p – 1)

Question 10.
Factorise : 3x³ – 45x²y + 225xy² – 375y³
Answer:
= 3x³ – 45x²y + 225xy² – 375y³
= 3(x³ – 15x²y + 75xy² – 125y³)
= 3(x³ – 3x²(5y) + 3x(5y)² – (5y)³)
= 3(x – 5y)³