Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.4 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.4
Question 1.
Factorise the following by taking out the common factor
(i) 18xy – 12yz
Answer:
18xy – 12yz = (2 × 3 × 3 × y × x) – (2 × 2 × 3 × y × z)
Taking out the common factors 2, 3, y, we get
= 2 × 3 × y(3x – 2z) = 6y(3x – 2z)
![]()
(ii) 9x5y3 + 6x3y2 – 18x2y
Answer:
9x5 + 6x3y2 – 18x2y = (3 × 3 × x2 × x3 × y × y) + (2 × 3 × x2 × x × y × y) – (2 × 3 × 3 × x2 × y)
Taking out the common factors 3, x2, y, we get
= 3 × x2 × y (3x3y2 + 2xy – 6)
= 3x2y (3x3y2 + 2xy – 6)
(iii) x(b – 2c) + y(b – 2c)
Answer:
Taking out the binomial factor (b – 2c) from each term, we have
= (b – 2c)(x + y)
(iv)(ax + ay) + (bx + by)
Answer:
Taking at ‘a’ from the first term and ‘b’ from the second term we have
(ax + ay )+ (bx + by) = a(x + y) + b(x + y)
Now taking out the binomial factor (x + y) from each term
= (x + y) (a + b)
![]()
(v) 2x2(4x – 1) – 4x + 1
Answer:
Taking out -1 from last two terms
2x2 (4x – 1) – 4x + 1 = 2x2 (4x – 1) – 1 (4x – 1)
Taking out the binomial factor 4x – 1, we get
= (4x – 1) (2x2 – 1)
(vi) 3y(x – 2)2 – 2(2 – x)
Answer:
3y(x – 2)2 – 2(2 – x) = 3y(x – 2)(x – 2) – 2( -1)(x – 2)
[∵ Taking out – 1 from 2 – x]
= 3y(x – 2)(x – 2) + 2(x – 2)
Taking out the binomial factor x – 2 from each term, we get
= (x – 2) [3y(x – 2) + 2]
(vii) 6xy – 4y2 + 12xy – 2yzx
Answer:
= 6xy + 12xy – 4y2 – 2yzx [∵ Addition is commutative]
= (6 × x × y) + (2 × 6 × x × y) + (-1) (2) (2) y + y) + ((-1) (2) (y) (z) (x))
Taking out 6 x x x y from first two terms and (-1) × 2 × y from last two terms we get
= 6 × x × y(1 + 2) + (-1) (2) y [2y + zx]
= 6 × y(3) – 2y(2y + zx)
= (2 × 3 × 3 × x × y) – 2xy(2y + zx)
Taking out 2y from two terms
= 2y(9x – (2y + zx))
= 2y (9x – 2y – xz)
![]()
(viii) a3 – 3a2 + a – 3
Answer:
a2 – 3a2 + a – 3 = a2(a – 3) + 1(a – 3) [:Groupingthetermssuitably]
= (a – 3) (a2 + 1)
(ix) 3y3 – 48y
Answer:
3y2 – 48y = 3 × y × y2 – 3 × l6 × y
Taking out 3 × y
= 3y(y2 – 16) = 3y(y2 – 42)
Comparing y2 – 42 with a2 – b2
a = y, b = 4
a2 – b2 = (a + b) (a – b)
y2 – 42 = (y + 4) (y – 4)
∴ 3y(y2 – 16) = 3y(y + 4)(y – 4)
(x) ab2 – bc2 – ab + c2
Answer:
ab2 – bc2 – ab + c2
Grouping suitably
ab2 – bc2 – ab + c2 = b (ab – c2) – 1 (ab – c2)
Taking out the binomial factor ab – c2 = (ab – c2) (b – 1)
![]()
Question 2.
Factorise the following expressions
(i) x2 + 14x + 49
Answer:
x2 + 14x + 49 = x2 + 14x + 72
Comparing with a2 + 2ab + b2 = (a + b)2 we have a = x and b = 7
⇒ x2 + 2(x)(7) + 72 = (x + 7)2
∴ x2 + 14x + 49 = (x + 7)2
(ii) y2 – 10y + 25
Answer:
y2 – 10y + 25 = y2 – 10y + 52
Comparing with a2 – 2ab + b2 = (a – b)2 we get a = y; b = 5
⇒ y2 – 2(y) (5) + 52 = (y – 5)2
∴ y2 – 10y + 25 = (y – 5)2
(iii) c2 – 4c – 12
Answer:
This is of the form ax2 + bx + c
Where a = 1, b = -4 c = -12, x = c
Now the product ac = 1 × – 12 = -12 and the sum b = -4
| Product = – 72 | Sum = 1 |
| 1 × (-12) = -12 | 1 + (-12) = -11 |
| 2 × (-6) = – 12 | 2 + (-6) = – 4 |
∴ The middle term – 4c can be written as 2c – 6c
∴ c2 – 4c – 12 = c2 + 2c – 6c – 12
= c(c + 2) -6 (c + 2)
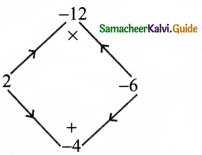
Taking out (c + 2)
⇒ (c + 2)(c – 6)
∴ c2 – 4c – 12 = (c + 2)(c – 6)
![]()
(iv) m2 + m – 72
Answer:
m2 + m – 72
This is of the form ax + bx + c
where a = 1, b = 1, c = -72
| Product = – 72 | Sum = 1 |
| 1 × -72 = – 72 | 1 + (-72) = -71 |
| 2 × – 36 = – 72 | 2 + (-36) = – 34 |
| 3 × (-24) = – 72 | 3 + (-24) = – 21 |
| 4 × (-18) = -72 | 4 + (-18) = – 14 |
| 6 × (-12) = -72 | 6 + (-12) = – 6 |
| 8 × (-9) = -72 | 8 + (-9) = – 1 |
| 9 × (-8) = – 72 | 9 + (-8) = 1 |
Product a × c = 1 × -72 = -72
Sum b = 1
The middle term m can be written as 9m – 8m
m2 + m – 72 = m2 + 9m – 8m – 72
= m(m + 9) – 8(m + 9)
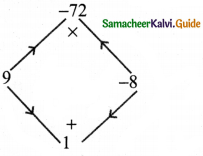
Taking out (m + 9)
= (m + 9)(m – 8)
∴ m2 + m – 72 = (m + 9)(m – 8)
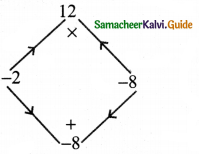
(v) 4x2 – 8x + 3
Answer:
4x2 – 8x + 3
This is of the form ax2 + bx + c with a = 4 b = -8 c = 3
Product ac = 4 × 3 = 12
sum b = -8
| Product = 12 | Sum = -8 |
| (-1) × (-12) = 12 | (-1) + (-12) = – 13 |
| (-2) × (-6) = 12 | (-2) + (-6) = – 8 |
The middle term can be written as – 8x = – 2x – 6x
4x2 – 8x + 3 = 4x2 – 2x – 6x + 3
= 2x (2x – 1) – 3 (2x – 1)
= (2x – 1)(2x – 3)
4x2 – 8x + 3 = (2x – 1) (2x – 3)
![]()
Question 3.
Factorise the following expressions using (a + b)3 = a3 + 3a2b + 3ab2 + b3 identity
(i) 64x3 + 144x2 + 108x + 27
(ii) 27p3 + 54p3q + 36pq2 + 8q3
Answer:
(i) 64x3 + 144x2 + 108x + 27
= (4x)3 + 3(4x)2 (3) + 3(4) (3)2 + 33
= (4x + 3)3
(ii) 27p3 + 54p3q + 36pq2 + 8q3
= (3p)3 + 3(3p)2 (2q) + 3(3p) (2q)2 + (2q)3
= (3p + 2q)3
![]()
Question 4.
Factorise the following expressions using (a – b)3 = a3 – 3a2b + 3ab2 – b3 identity
(i) y3 – 18y2 + 108y – 216
(ii) 8m3 – 60m2n + 150mn2 – 125n3
Answer:
(i) y3 – 18y2 + 108y – 216
= y3 – 3y2(6) + 3(6)2y – 63
= (y – 6)3
(ii) 8m3 – 60m2n + 150mn2 – 125n3
= (2m)3 – 3(2m)2 (5) + 3(2m)(5n)2 – (5n)3
= (2m – 5n)3