Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 1 Numbers Ex 1.1 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 1 Numbers Ex 1.1
Question 1.
Fill in the blanks:
(i) \(\frac{-19}{5}\) lies between the integers _________ and _________ .
Answer:
-4 and -3
(ii) The decimal form of the rational number \(\frac{15}{-4}\) is _________ .
Answer:
-3.75
![]()
(iii) The rational numbers \(\frac{-8}{3}\) and \(\frac{8}{3}\) are equidistant from _________.
Answer:
0
(iv) The next rational number in the sequence \(\frac{-15}{24}, \frac{20}{-32}, \frac{-25}{40}\) is _________.
Answer:
\(\frac{30}{-48}\)
(v) The standard form of \(\frac{58}{-78}\) is _________.
Answer:
\(\frac{-29}{39}\)
Question 2.
Say True or False
(i) 0 is the smallest rational number.
Answer:
False
(ii) \(\frac{-4}{5}\) lies to the left of \(\frac{-3}{4}\).
Answer:
True
(iii) \(\frac{-19}{5}\) is greater than \(\frac{15}{-4}\).
Answer:
False
(iv) The average of two rational numbers lies between them.
Answer:
True
(v) There are an unlimited number of rational numbers between 10 and 11.
Answer:
True
![]()
Question 3.
Find the rational numbers represented by each of the question marks marked on the following number lines.
(i)

Answer:
The number lies between —3 and 4. The unit part between -3 and -4 is divided into 3 equal parts and the second part is asked.
∴ The required number is -3 \(\frac{2}{3}=-\frac{11}{3}\)
(ii)

Answer:
The required number lies between 0 and -1. The unit part between 0 and -1 is divided
into 5 equal parts, and the second part is taken.
∴ The required number is \(-\frac{2}{5}\)
(iii)

Answer:
The required number lies between 1 and 2. The unit part between 1 and 2 is divided into 4 equal parts and the third part is taken.
∴ The required number is 1\(\frac{3}{4}=\frac{7}{4}\)
Question 4.
The points S, Y, N, C, R, A, T, I and O on the number line are such that CN=NY=YS and RA=AT=TI=IO. Find the rational numbers represented by the letters Y, N, A, T and I.
![]()
Answer:

![]()
Question 5.
Draw a number line and represent the following rational numbers on it.
(i) \(\frac{9}{4}\)
(ii) \(\frac{-8}{3}\)
(iii) \(\frac{-17}{-5}\)
(iv) \(\frac{15}{-4}\)
Answer:
(i) \(\frac{9}{4}\)
\(\frac{9}{4}=2 \frac{1}{4}\)
∴ \(\frac{9}{4}\) lies between 2 and 3

(ii) \(\frac{-8}{3}\)
\(\frac{-8}{3}=-2 \frac{2}{3}\)
\(-2 \frac{2}{3}\) lies between -2 and 3

(iii) \(\frac{-17}{-5}\)
\(\frac{-17}{-5}=3 \frac{2}{5}\)
\(3 \frac{2}{5}\) lies between 3 and 4 in the number line.

(iv) \(\frac{15}{-4}\)
\(\frac{15}{-4}=-3 \frac{3}{4}\)
\(-3 \frac{3}{4}\) lies between -3 and -4

![]()
Question 6.
Write the decimal form of the following rational numbers.
(i) \(\frac{1}{11}\)
(ii) \(\frac{13}{4}\)
(iii) \(\frac{-18}{7}\)
(iv) \(1 \frac{2}{5}\)
(v) \(-3 \frac{1}{2}\)
Answer:
(i) \(\frac{1}{11}\)
\(\frac{1}{11}\) = 0.0909….

(ii) \(\frac{13}{4}\)
\(\frac{13}{4}\) = 3.25

![]()
(iii) \(\frac{-18}{7}\)
\(\frac{-18}{7}\) = -2.571428571428….

(iv) \(1 \frac{2}{5}\)
\(1 \frac{2}{5}=\frac{7}{5}\) = 1.4
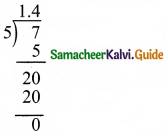
(v) \(-3 \frac{1}{2}\)
\(-3 \frac{1}{2}=-\frac{7}{2}=-3.5\)
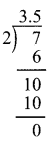
![]()
Question 7.
List any five rational numbers between the given rational numbers.
(i) 2 and 0
(ii) \(\frac{-1}{2}\) and \(\frac{3}{5}\)
(iii) \(\frac{1}{4}\) and \(\frac{7}{20}\)
(iv) \(\frac{-6}{4}\) and \(\frac{-23}{10}\)
Answer:
(i) 2 and 0
i.e., \(\frac{-2}{1}\) and \(\frac{0}{1}\)
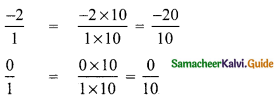
∴ Five rational number between \(\frac { -20 }{ 10 }\) (= -2) and \(\frac { 0 }{ 10 }\) (= 0) are
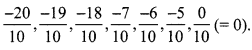
(ii) \(\frac{-1}{2}\) and \(\frac{3}{5}\)
LCM of 2 and 5 = 2 × 5 = 10
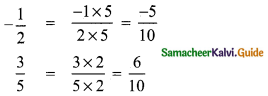
∴ Five rational number between
![]()
![]()
(iii) \(\frac{1}{4}\) and \(\frac{7}{20}\)
![]()
∴ Five rational number between
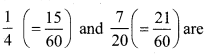
![]()
(iv) \(\frac{-6}{4}\) and \(\frac{-23}{10}\)
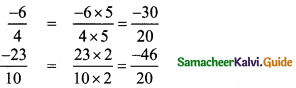
∴ Five rational number between
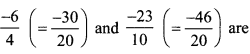
![]()
![]()
Question 8.
Use the method of averages to write 2 rational numbers between \(\frac{14}{5}\) and \(\frac{16}{3}\)
Answer:
The average of a and b is \(\frac { 1 }{ 2 }\)(a + b)
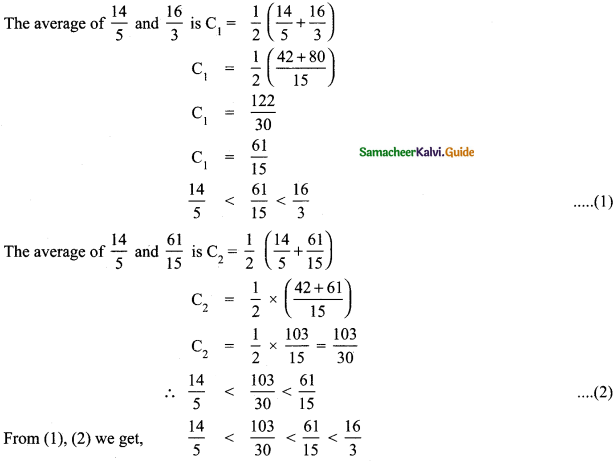
![]()
Question 9.
Compare the following pairs of rational numbers.
(i) \(\frac{-11}{5}, \frac{-21}{8}\)
(ii) \(\frac{3}{-4}, \frac{-1}{2}\)
(iii) \(\frac{2}{3}, \frac{4}{5}\)
Answer:
(i) \(\frac{-11}{5}, \frac{-21}{8}\)
LCM of 5, 8 is 40
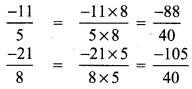
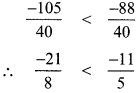
(ii) \(\frac{3}{-4}, \frac{-1}{2}\)
LCM of 4 and 2 = 4
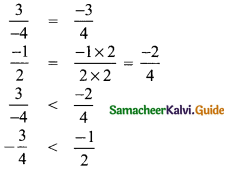
![]()
(iii) \(\frac{2}{3}, \frac{4}{5}\)
LCM of 3 and 5 is 15.
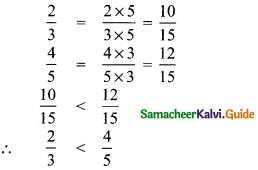
Question 10.
Arrange the following rational numbers in ascending and descending order.
(i) \(\frac{-5}{12}, \frac{-11}{8}, \frac{-15}{24}, \frac{-7}{-9}, \frac{12}{36}\)
(ii) \(\frac{-17}{10}, \frac{-7}{5}, 0, \frac{-2}{4}, \frac{-19}{20}\)
Answer:
(i) \(\frac{-5}{12}, \frac{-11}{8}, \frac{-15}{24}, \frac{-7}{-9}, \frac{12}{36}\)
LCM of 12, 8, 24, 9, 36 is 4 × 3 × 2 × 3 = 72

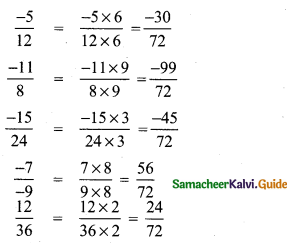
Now comparing the numerators – 30, – 99, -45, 56, 24 we get 56 > 24 > – 30 > – 45 > – 99
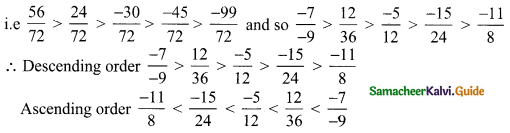
![]()
(ii) \(\frac{-17}{10}, \frac{-7}{5}, 0, \frac{-2}{4}, \frac{-19}{20}\)
LCM of 10, 5, 4, 20 is 5 × 2 × 2 = 20

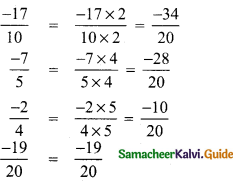
Negative numbers are less than zero.
∴ Arranging the numerators we get
– 34 < – 28 < – 19 < – 10 < 0
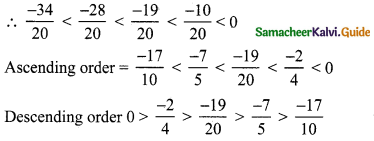
![]()
Objective Type Questions:
Question 11.
The number which is subtracted from \(\frac{-6}{11}\) to get \(\frac{8}{9}\) is _________ .
(A) \(\frac{34}{99}\)
(B) \(\frac{-142}{99}\)
(C) \(\frac{142}{99}\)
(D) \(\frac{-34}{99}\)
Answer:
(B) \(\frac{-142}{99}\)
Hint:
Let x be the number to be subtracted
\(\frac{-6}{11}-x\) = \(\frac{8}{9}\)
\(\frac{-6}{11}-\frac{8}{9}\) = x
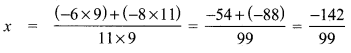
Question 12.
Which of the following pairs is equivalent?
(A) \(\frac{-20}{12}, \frac{5}{3}\)
(B) \(\frac{16}{-30}, \frac{-8}{15}\)
(C) \(\frac{-18}{36}, \frac{-20}{44}\)
(D) \(\frac{7}{-5}, \frac{-5}{7}\)
Answer:
(B) \(\frac{16}{-30}, \frac{-8}{15}\)
Hint:
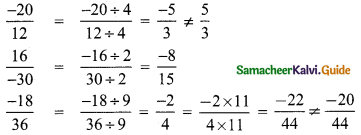
∴ \(\frac{16}{-30}\) and \(\frac{-8}{15}\)
![]()
Question 13.
\(\frac{-5}{4}\) is a rational number which lies between _________ .
(A) 0 and \(\frac{-5}{4}\)
(B) -1 and 0
(C) -1 and -2
(D) -4 and -5
Answer:
(C) -1 and -2
Hint:
\(\frac{-5}{4}\) = -1 \(\frac{1}{4}\)
∴ \(\frac{-5}{4}\) lies between -1 and -2.
Question 14.
Which of the following rational numbers is the greatest?
(A) \(\frac{-17}{24}\)
(B) \(\frac{-13}{16}\)
(C) \(\frac{7}{-8}\)
(D) \(\frac{-31}{32}\)
Answer:
(A) \(\frac{-17}{24}\)
Hint:
LCM of 24, 16, 8, 32 = 8 × 2 × 3 × 2 = 96

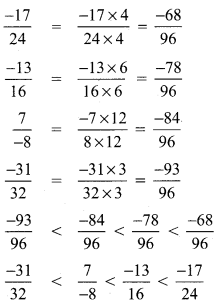
∴ \(\frac{-17}{24}\) is the greatest number
![]()
Question 15.
The sum of the digits of the denominator in the simplest form of is \(\frac{112}{528}\) is _________ .
(A) 4
(B) 5
(C) 6
(D )7
Answer:
(C) 6
Hint:
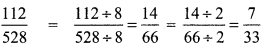
Sum of digits in the denominator = 3 + 3 = 6