Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.1 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.1
Question 1.
Find the adjoint of the following:
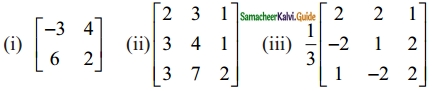
Solution:
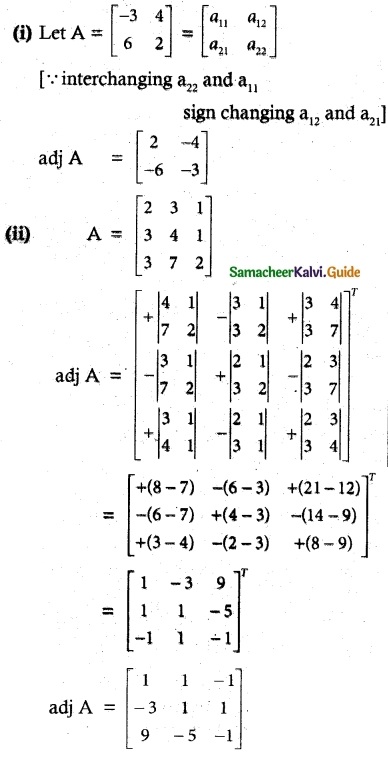

![]()
Question 2.
Find the inverse (if it exists) of the following.
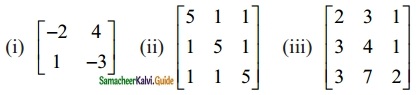
Solution:
\(\begin{bmatrix} -2 & 4 \\ 1 & -3 \end{bmatrix}\)
|A| = 6 – 4 = 2 ≠ 0
∴ A-1 exists. A is non singular.
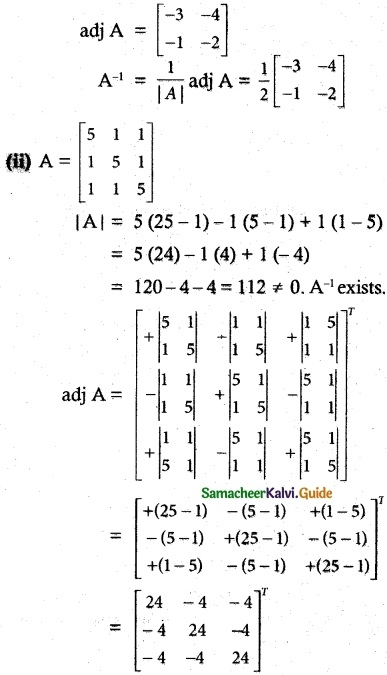
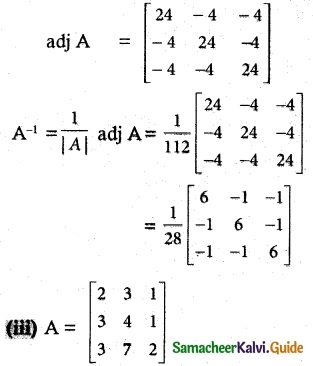
|A| = 2(8-7)-3(6-3)+1(21-12)
= 2 – 9 + 9 = 2 ≠ 0. A-1 exists.
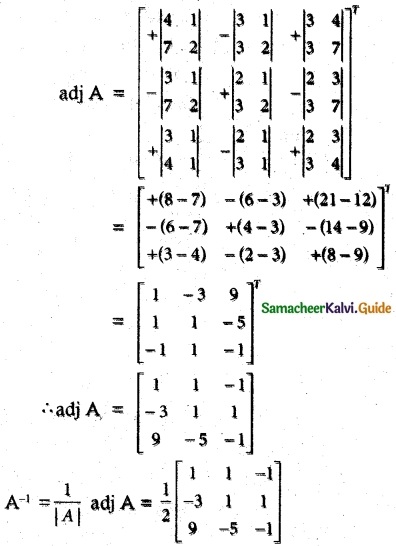
![]()
Question 3.
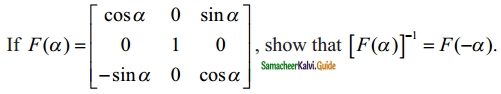
Solution:
\(\left[\begin{array}{ccc}
\cos \alpha & 0 & \sin \alpha \\
0 & 1 & 0 \\
-\sin \alpha & 0 & \cos \alpha
\end{array}\right]\)
|F(α)| = cos α(cos α – 0) – 0 + sin α(0 + sin α)
= cos²α + sin²α = 1
|f(α)| = 1 ≠ 0. [F(α)]-1 exists.

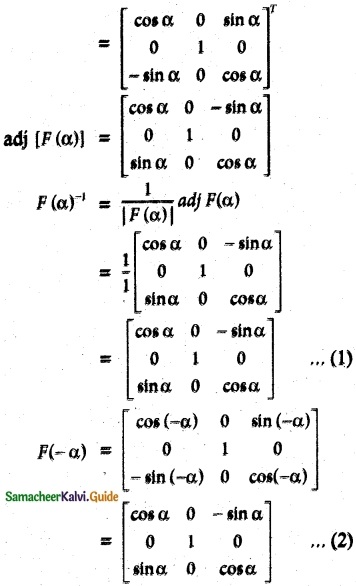
[∵ cos (-θ) = cos θ ; sin(-θ) = -sin θ]
from (1) and (2) we have
[F(α)]-1 = F(-α)
![]()
Question 4.
If A = \(\begin{bmatrix} 5 & 3 \\ -1 & -2 \end{bmatrix}\), show that A² – 3A – 7I2 = O2. hence find A-1
Solution:
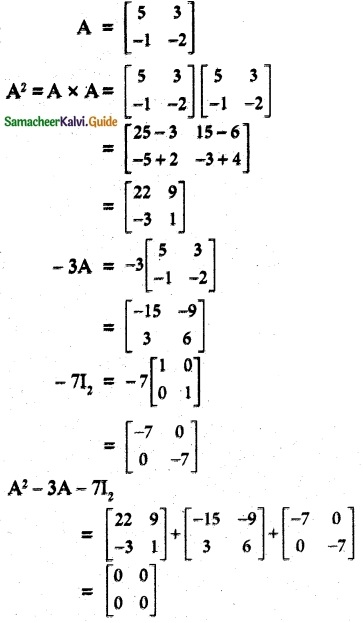
∴ A² -3A – 7I2 = O2
Post multiply this equation by A-1
A2A-1 – 3A A-1 – 7I2 A-1 = 0
A – 3I – 7A-1 = 0
A – 3I = 7 A-1
A-1 = \(\frac {1}{7}\) (A – 3I)
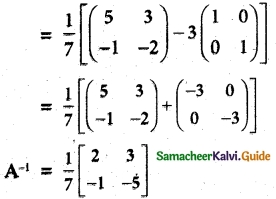
Question 5.
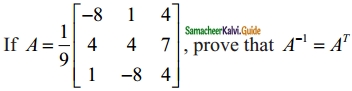
Solution:
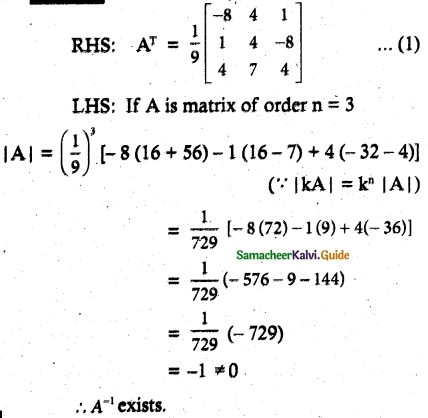

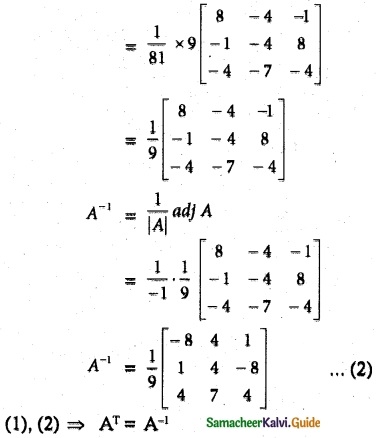
![]()
Question 6.
If A = \(\begin{bmatrix} 8 & -4 \\ -5 & 3 \end{bmatrix}\) verify that A(adj A) = (adj A) A = \(\left| A \right|\)I2.
Solution:

(1), (2) and (3) ⇒ A (adj A) = (adj A)A = |A| I2.
Question 7.
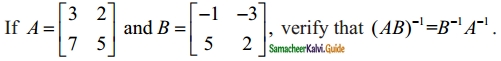
Solution:

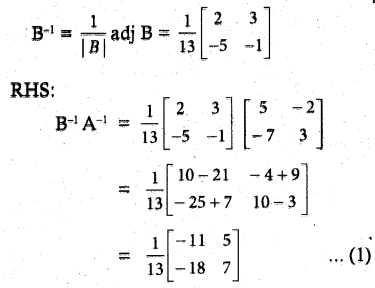

![]()
Question 8.
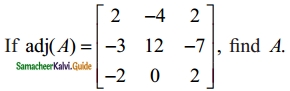
Solution:
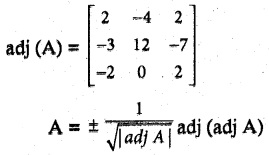
|adj (A)| = 2 (24 – 0) + 4 (- 6 – 14) + 2(0 + 24)
= 48 – 80 + 48 = 16

Question 9.
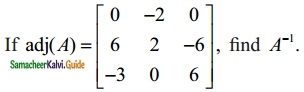
Solution:
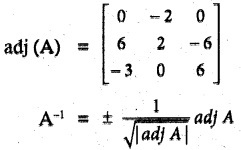
|adj A| = 0 + 2(36 – 18) + 0 = 2(18) = 36
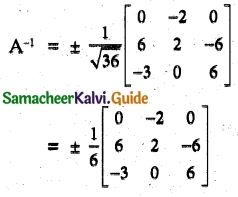
![]()
Question 10.
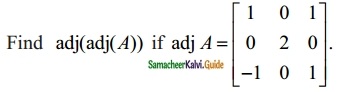
Solution:

Question 11.

Solution:
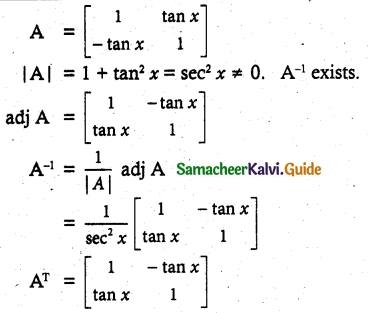
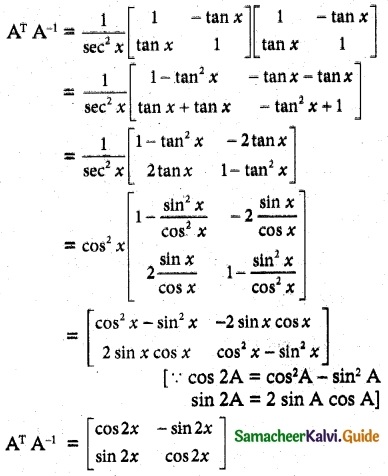
Hence proved
![]()
Question 12.
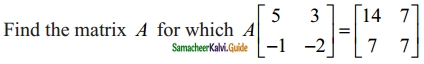
Solution:

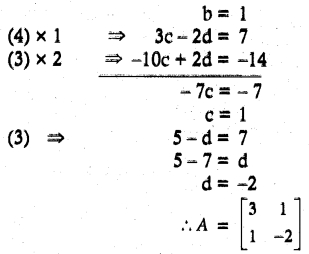
![]()
Question 13.
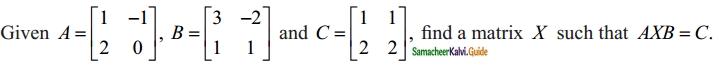
Solution:
Given A × B × C
⇒ A-1 A × B B-1 = A-1 C B-1
I × I = A-1 C B-1
⇒ X = A-1 CB-1
let us find A-1 and B-1

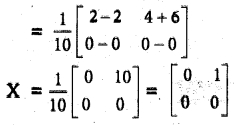
![]()
Question 14.

Solution:

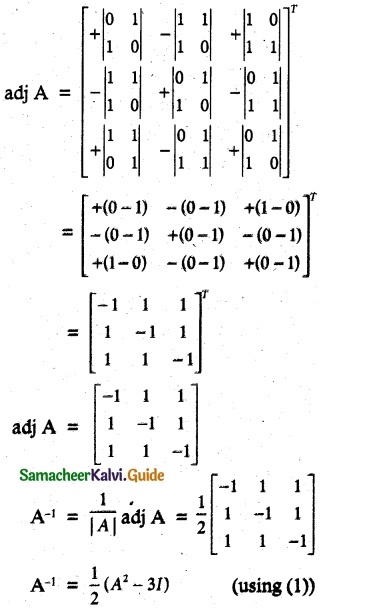
Hence proved.
![]()
Question 15.
Decrypt the received encoded message [2 -3] [20 4] with the encryption matrix \(\begin{bmatrix} -1 & -1 \\ 2 & 1 \end{bmatrix}\) and the decryption matrix as its inverse, where the system of codes are described by the numbers 1 – 26 to the letters A – Z respectively, and the number 0 to a blank space.
Solution:

So the sequence of decoded row matrics is [8 5] [12 16]
The receiver reads the message as “HELP”.